Chapters
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Exercise 12
- Exercise 13
- Exercise 14
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9
- Solution of exercise 10
- Solution of exercise 11
- Solution of exercise 12
- Solution of exercise 13
- Solution of exercise 14
Exercise 1
Determine the quadratic equation whose solutions are 3 and −2.
Exercise 2
Factor:
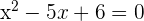
Exercise 3
Determine the value of k so that the two roots of the equation x² − kx + 36 = 0 are equal.
Exercise 4
The sum of two numbers is 5 and their product is −84. Find these numbers.
Exercise 5
Within 11 years, the age of Peter will be half the square of the age he was 13 years ago. Calculate the current age of Peter.
Exercise 6
To fence a rectangular farm of 750 m², 110 m of fence has been used. Calculate the dimensions of the farm.
Exercise 7
The three sides of a right-angled triangle are proportional to the numbers 3, 4 and 5. Find the length of each side knowing that the area of the triangle is 24 m².
Exercise 8
A rectangular garden 50 m long and 34 m wide is surrounded by a uniform dirt road. Find the width of the road if the total area of the garden and road is 540 m².
Exercise 9
Calculate the dimensions of a rectangle whose diagonal is 75 m, knowing that is similar to a rectangle with sides measuring 36 m 48 m respectively.
Exercise 10
Two natural numbers differ by two units and the sum of their squares is 580. What are these numbers?
Exercise 11
Two taps A and B fill a swimming pool together in two hours. Alone, it takes tap A three hours less than B to fill the same pool. How many hours does it take each tap to fill the pool separately?
Exercise 12
The length of the sides of a right-angled triangle are measured as three consecutive even numbers (in cm). Find the values of these sides.
Exercise 13
A rectangular piece of cardboard is 4 cm longer than wide. A box of 840 cm³ is constructed by using this piece of cardboard. A square of 6 cm is cut out in every corner and the rims are folded upwards to create the box. Find the dimensions of the box.
Exercise 14
2 faucets can fill a tank in 1 hour and 20 minutes. The first faucet takes more than two hours longer to fill the same tank when functioning without the second tap. How long does it take to fill each one separately?
Find the best Maths tutor on Superprof.
Solution of exercise 1
Determine the quadratic equation whose solutions are: 3 and −2.
S = 3 − 2 = 1
P = 3 · 2 = 6
x² − x + 6 = 0
Solution of exercise 2
Factor:
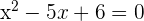
Solution of exercise 3
Determine the value of k so that the two roots of the equation x² − kx + 36 = 0 are equal.
Find more learn Maths online here on Superprof.
Solution of exercise 4
The sum of two numbers is 5 and their product is −84. Find these numbers.
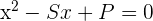
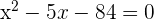
Solution of exercise 5
Within 11 years, the age of Peter will be half the square of the age he was 13 years ago. Calculate the current age of Peter.
Current age x
Age 13 years ago x − 13
Age within 11 years x + 11
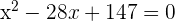
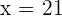
Current age 21
Solution of exercise 6
To fence a rectangular farm of 750 m², 110 m of fence has been used. Calculate the dimensions of the farm.
Semiperimeter 55
Base x
Height 55 − x
x · (55 − x) = 750
x² − 55x + 750 = 0
x = 25 x = 30
The dimensions of the farm are 30 m and 25 m.
Solution of exercise 7
The three sides of a right-angled triangle are proportional to the numbers 3, 4 and 5. Find the length of each side knowing that the area of the triangle is 24 m².
1st side (base) 3x
2nd side (height) 4x
3rd side 5x
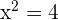
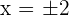
1st side 6 m
2nd side 8 m
3rd side 10 m
Solution of exercise 8
A rectangular garden 50 m long and 34 m wide is surrounded by a uniform dirt road. Find the width of the road if the total area of the garden and road is 540 m².
(50 + 2x) · (34 + 2x) − 50 · 34 = 540
4x² + 168x − 540 = 0 x² + 42x − 135 = 0
x = 3 and x = −45
The road width is 3 m .
Check for many great maths tutors in the UK here.
Solution of exercise 9
Calculate the dimensions of a rectangle whose diagonal is 75 m, knowing that it is similar to a rectangle with sides measuring 36 m 48 m respectively.
Base 48x : 12 = 4x
Height 36x : 12 = 3x
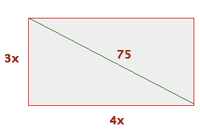
(4x)² + (3x)² = 75²
25x² = 5625
x² = 225 x = 15
Base 4 · 15 = 60 m
Height 3 · 15 = 45 m
Solution of exercise 10
Two natural numbers differ by two units and the sum of their squares is 580. What are these numbers?
1st number x
2nd number x + 2
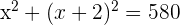
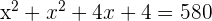
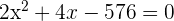
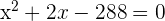
1st number 16
2nd number 18
Solution of exercise 11
Two taps A and B fill a swimming pool together in two hours. Alone, it takes tap A three hours less than B to fill the same pool. How many hours does it take each tap to fill the pool separately?
Time of A x
Time of B x + 3
A
B
A and B
LCM(2, x, x + 3) = 2x (x + 3)
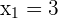
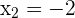
Time of A 3 hours
Time of B 6 hours
Solution of exercise 12
The length of the sides of a right-angled triangle are measured as three consecutive even numbers (in cm). Find the values of these sides.
1st leg 2x
2nd leg 2x + 2
Hypotenuse 2x + 4
(2x)² + (2x + 2)² = (2x + 4)²
4x² + 4x² + 8x + 4 = 4x² + 16x + 16
4x² − 8x − 12 = 0 x² − 2x − 3 = 0
x = 3 y x= −1
1st leg 6 cm
2nd leg 8 cm
Hypotenuse 10 cm
Solution of exercise 13
A rectangular piece of cardboard is 4 cm longer than wide. A box of 840 cm³ is constructed by using this piece of cardboard. A square of 6 cm is cut out in every corner and the rims are folded upwards to create the box. Find the dimensions of the box.
6 (x − 12) · (x + 4 −12) = 840 (x − 12) · (x −8) = 140
x² − 20x − 44 = 0 x = 22 y x= −2
The dimensions are: 26 cm and 22 cm.
Solution of exercise 14
2 faucets can fill a tank in 1 hour and 20 minutes. The first faucet takes more than two hours longer to fill the same tank when functioning without the second tap. How long does it take to fill each one separately?
1st Time x
2nd Time x − 2
1º
2º
Between the two
1st Time 4 hours
2nd Time 2 hours
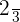is not a solution because the time for the second faucet would be negative.
Did you like this article? Rate it!
Loading...
3^x -2^y+2=10
2^x-3^x-2=2