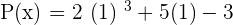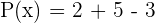The word polynomial can be broken into two words. One is "poly" and another is the "nominal". The word "poly" means more than "one" and the word "nominal" means more than one term. It means that any equation that has more than one term is called a polynomial equation. We usually relate polynomial equations with the degree of monomials but let's stick with polynomial, for now, we will discuss that later in this lesson. A polynomial is an algebraic expression in the form:
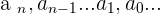are the numbers and are called coefficients.
n is a natural number.
x is the variable.
ao is the independent term.
Whenever you will encounter any polynomial equation, you will notice three things, one is the variable, the other is the constant, and the last is the exponent (or power). These three things are common in a polynomial equation, below are some examples of polynomial equations:
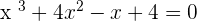
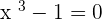
The above equations are polynomial equations but with different degrees and for each degree, there is a different method to solve. Furthermore, for each degree, the graph of that polynomial will also be different, however, if the degrees are the same, the graph will be similar which means you can predict the graph. For example, the graph of linear equation will be a straight line but that straight line can be at a certain angle from normal or at a different position but one thing is for sure and that is the line will be straight. That is how you can predict the line of the equation just by look at its degree.
Degree of a Polynomial
The degree of a polynomial P(x) is the greatest degree of the monomials.
Classification of a Polynomial According to Their Degree
Polynomials are classified according to their degree. This helps mathematicians to understand them more clearly. Below are all the types of polynomials:
Straight Line
Straight-line equations mostly contain two terms with the degree of 
. That means the power of variable/s will not be more than .
Find more Maths tutor here on Superprof.
Quadratic
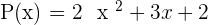
If the equation has a variable with maximum power equal to 2 that means you are dealing with a quadratic equation. In the above equation, there are three terms, if you look at the first term, it has a variable and the power of that variable is 
.
Cubic
In the case of cubic equation, you will see a variable having a power of 
. If the equation has a variable with maximum power 
that means that it is an cubic equation.
Quartic
As the word tells you that the maximum power of this polynomial will be .
Quintic
Equations that has polynomial degree 
is called a quintic equation.
Sextic
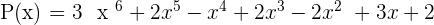
Sextic equation has a polynomial degree 
.
Find the best Maths tutors on Superprof.
Types of Polynomials
Classification and types are two different things. There are seven types of polynomials that you can encounter. Below are all the types of polynomials:
Zero Polynomial
A polynomial that has zero as all its coefficients.
Homogeneous Polynomial
A polynomial where all its terms or monomials are of the same degree.
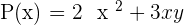
Complete Polynomial
A polynomial that has all the terms ordered from the greatest degree up to the independent degree.
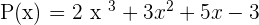
Ordered Polynomial
A polynomial that has its monomials ordered starting from the greatest or smallest degree.
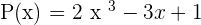
Equal Polynomials
For the case of equal polynomials, there are two conditions. Two polynomials are equal if:
Condition no.1
The two polynomials have the same degree.
Condition no.2
The coefficients of the terms with the same degree are equal.
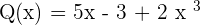
Similar Polynomials
Two polynomials are similar if they have the same literal part.
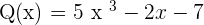
Evaluating Polynomials
Evaluating a polynomial is to find its numerical value when the variable x is replaced by any number.
Supposing 
:
Did you like this article? Rate it!
Loading...
