Chapters
Exercise 1
Indicate which of the following expressions are monomials. If it is, indicate the degree and coefficient of the monomial. If it is not, state why it is not a monomial:
1 
2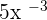 
3 
4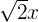 
5 
6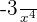 
7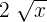 
Exercise 2
Simplify:
1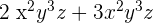 
2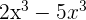 
3 
4 
Exercise 3
Solve:
1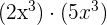 
2 
3 
4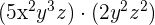 
5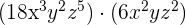 
6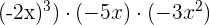 
Exercise 4
Solve:
1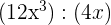 
2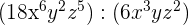 
3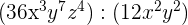 
4 
5 
6 
Exercise 5
Solve:
1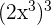 
2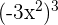 
3 
Solution of exercise
Solution of exercise 1
Indicate which of the following expressions are monomials. If it is, indicate the degree and coefficient of the monomial. If it is not, state why it is not a monomial:
1
Degree : 3, coefficient : 3
2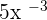
It is not a monomial because the exponent is not a natural number
3
It is a binomial, not a monomial.
4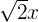
Degree : 1, coefficient 
5
Degree:4, coefficient :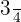 
6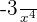
It is not a monomial because the exponent is not a natural number.
7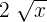
It is not a monomial because the variable is inside the root.
Solution of exercise 2
Simplify:
1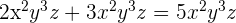 
2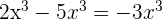 
3 
4 
Solution of exercise 3
Solve:
1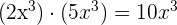 
2 
3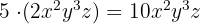 
4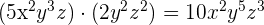 
5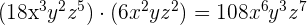 
Solution of exercise 4
Solve:
1 
2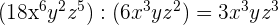 
3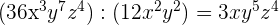 
4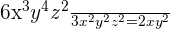 
5 
6 
Solution of exercise 5
Solve:
1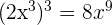 
2 
3 
Did you like this article? Rate it!
Loading...
