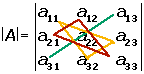Chapters
In this resource, we have compiled all the formulas related to algebra. Algebra is a field of mathematics in which we study mathematical symbols and those rules that manipulate these symbols. These symbols in elementary algebra reflect the quantities that have no fixed values. These quantities are known as variables. The relationship between different variables in algebra is depicted through equations. The arithmetic operations of addition, subtraction, multiplication, and division can be employed to solve complex problems in mathematics.

Monomials
- When we multiply two monomials together, we get a new monomial.
- When a monomial is multiplied by a constant, the resulting expression is also a monomial.
Now, let us see what are some of the common monomial formulas:
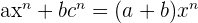


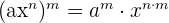
Binomials
Unlike a monomial, a binomial expression contains two terms. Any expression that has more than one term is also known as a polynomial. Hence, we can say that a binomial is a polynomial expression. A binomial is a combination of variables and constants. For instance, 3x + 5, 7xy - 9, and 2z + 1 are examples of binomial expressions. The terms in a binomial expression are segregated by the arithmetic operations of addition or subtraction. To be a binomial, an expression should fulfill the following conditions:
- It must have two terms
- If the variables of the two terms are the same, then their exponents (powers) must be different
- The exponents of the variables must be positive integers. They should not be fractions or negative integers.
One rule of a binomial expression is that the exponents of the same variables in a single term should be different. What does it mean? Let suppose, we have the following expression with two terms that have the same variables and their exponents.
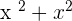
Since the exponents and variables are the same, hence we can easily add the above terms and the resulting answer will be monomial.

So, to avoid this, the exponents of the same variables should be different in binomial expressions. For instance, consider the following expressions having two same variables, but different exponents:

We cannot add them together. So, it is a binomial.
Some of the common binomial formulas are given below:

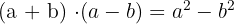

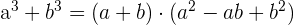

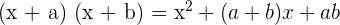
Find good maths tutors near me here.
Binomial Coefficient Formula
The general notation of the binomial coefficient is  . The formula for computing the binomial coefficient is given below:
. The formula for computing the binomial coefficient is given below:
 , where
, where 
It can be read as "n over k", or sometimes "n choose k".
It depicts the number of ways we can select unordered k number of outcomes from number of possibilities "n". The other formulas of binomial coefficient are:
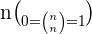

Trinomials
A trinomial is a polynomial expression that consists of three terms. These three terms are a combination of variables, constants, and coefficients multiplied together. Some examples of trinomial expressions are given below:

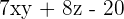
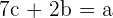
The formulas of trinomials are given below:
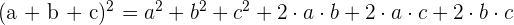

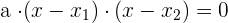
Quadratic Formula
To find a solution to a quadratic equation, we use the quadratic formula. The quadratic equation is an equation that has the highest power 2. The general form of quadratic equation is given below:
 ,
, 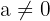
The formula to solve the above quadratic equation is given below:

If  , then
, then  .
.
If  , then
, then 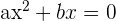


Matrix Formulas
Matrix is a set of numbers that are arranged into definite numbers of rows and columns. A matrix can be of an order 2x2, 3x3, 4x4, or so on. The matrix which has equal number of rows and columns is known as square matrix.
A matrix can have unequal number of rows and columns. This type of matrix is known as a rectangular matrix.
The common formulas of the matrices are given below:
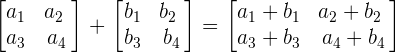

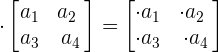
Find more Maths tutor here on Superprof.
Matrix Formulas

Inverse of a Matrix
The formula for computing the inverse of the matrix is given below:

Here, 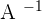 means inverse of the matrix A.
means inverse of the matrix A.
|A| means determinants of the matrix A
 Adjugate or cofactors of the matrix A
Adjugate or cofactors of the matrix A
 reflects transpose of the adjugate of matrix
reflects transpose of the adjugate of matrix
When a matrix is multiplied by its inverse, then we get an identity matrix.


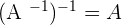
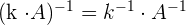
Determinants Formulas
Determinant of Order One
A matrix of order 1 has 1 row and 1 column in it. The determinant of the matrix of order 1 is the matrix itself:
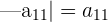
Determinant of Order Two
The determinant of the matrix of order two is calculated using the following formula:
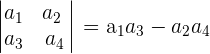
Determinant of Order Three
The determinant of the matrix of order 3 is computed using the following formula:

The determinant of the matrix B will be calculated as:
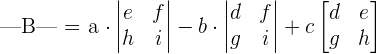
Rule of Sarrus
Rule of Sarrus is also called basketweave method. This rule presents an alternative way to compute the determinant of a 3x3 matrix.