Chapters

Exercise 1
Calculate the rank of the matrix

Exercise 2
Calculate the rank of the matrix by the gaussian elimination method.

Exercise 3
Calculate the rank of the matrix by the gaussian elimination method.
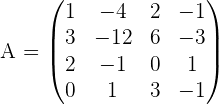
Exercise 4
Calculate the rank of the matrix by determinants.

Exercise 5
Calculate the rank of the matrix by determinants.
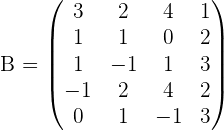
Exercise 6
Calculate the rank of the matrix by determinants.

Exercise 7
Calculate the rank of the matrix by determinants.

Solution of exercise 1
Calculate the rank of the matrix

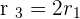
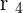 is null
is null
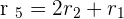
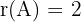
Solution of exercise 2
Calculate the rank of the matrix by the gaussian elimination method.



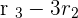
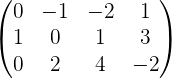
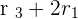

Therefore r(A) =2.
Solution of exercise 3
Calculate the rank of the matrix by the gaussian elimination method.
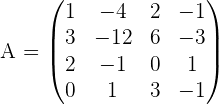
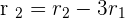
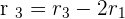

r(A) = 3.
Solution of exercise 4
Calculate the rank of the matrix by determinants.


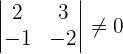

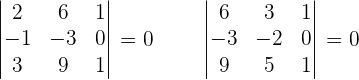
r(A) = 2
Solution of exercise 5
Calculate the rank of the matrix by determinants.



r(B) = 4
Solution of exercise 6
Calculate the rank of the matrix by determinants.

Remove the third column as it is zero, the fourth because it is proportional to the first and the fifth because it is the linear combination of the first and second: 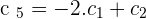
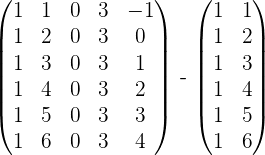

r(C) = 2
Solution of exercise 7
Calculate the rank of the matrix by determinants.

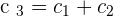


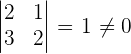
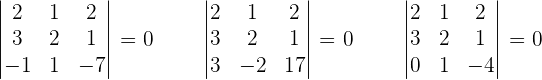
r(D) = 2













