Like every other operation, you can also multiply matrices. Although multiplication of matrices is a bit complex, once you understand the concept, it will be a piece of cake. There are a few types of multiplication of matrices such as scalar multiplication, n-tuples and the dot product, matrix and n-tuples, and matrix multiplication. These types are so versatile that they need a separate lesson but in this lecture, we will talk about matrices multiplication only.
You can multiply two or more matrices but there is a condition. If the rows and columns of all the matrices are equal then only you can perform the multiplication operation. To make it simple, suppose you have two matrices, matrix A and matrix B. To multiply matrix A and B, you need to check their rows as well as columns. If the rows and columns are the same in both matrices then only you can perform the multiplication operation. In short, two matrices A and B can be multiplied together if the number of columns of A is equal to the number of rows of B.
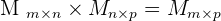
The element,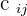 
, of the product matrix is obtained by multiplying every element in row i of matrix A by each element of column j of matrix B and then adding them together.
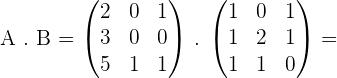
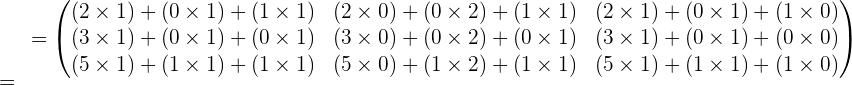
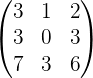
Properties of Matrix Multiplication
Property No. 1: Associative Property
It doesn't matter in which group you multiply the matrices, the answer will always be the same.
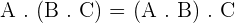
Property No. 2: Multiplicative Identity
This property states that if you multiply any matrix with an identity matrix, it will always result in the same matrix, the order of matrix doesn't matter.
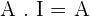
Where I is the identity matrix with the same order as matrix A.
Property No. 3: Not Commutative
The order of two matrices matters a lot.
Property No. 4: Distributive
Examples
Example 1
Given the matrices:
Calculate:
1. 
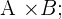
2. 
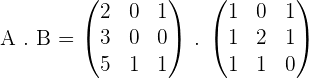
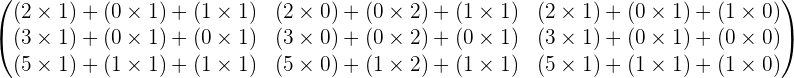
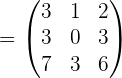
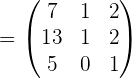
Example 2
Given the matrices:
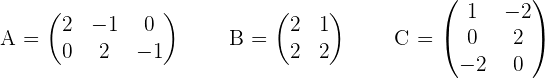
Determine if the following multiplications are possible:
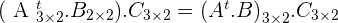
The multiplication is not possible because the number of columns,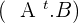 
does not coincide with the numbers of rows of 
.
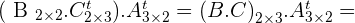
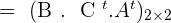
Determine the dimension of M so that the multiplication is possible: 
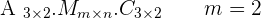
Determine the dimension of 
if 
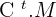is a square matrix.
Did you like this article? Rate it!
Loading...
