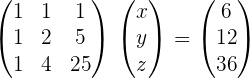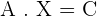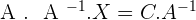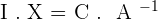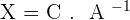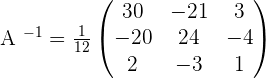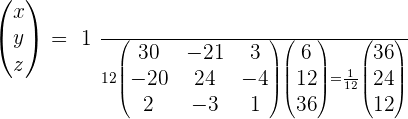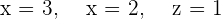To understand matrix equations, you should know how to multiply two matrices. Let's say you are showed the result of two matrices multiplication (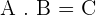 $\text{[math]}$ ) and you are asked to find the matrix B and you are provided matrix A and C, how will you find it? With the help of the matrix equation. In a matrix equation, the unknown is a matrix. This means that you will denote the unknown matrix as matrix X.

A · X = B

To solve, check that the matrix is invertible, if it is, premultiply (multiply to the left) both sides by the matrix inverse of A.

If the equation is of type X · A = B, the members must postmultiply (multiply to the right) because matrix multiplication is not commutative.

1. Given the matrices 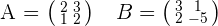$\text{[math]}$ . Solve the equation: A · X = B

$\text{[math]}$

Find the determinant of the above matrix.

$\text{[math]}$ $\text{[math]}$

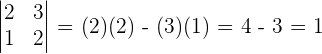
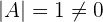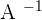
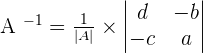
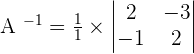
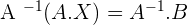
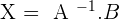
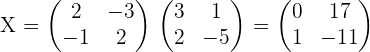
$\text{[math]}$ , this means that there is an inverse $\text{[math]}$

$\text{[math]}$ $\text{[math]}$ $\text{[math]}$

$\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$

2. Given the matrices 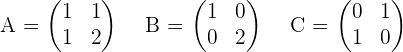$\text{[math]}$ . Solve the equation: X · A + B = C

$\text{[math]}$ $\text{[math]}$

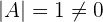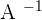
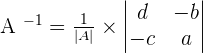
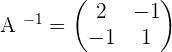
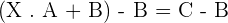
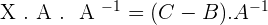
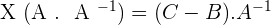
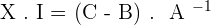
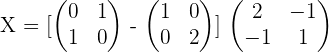
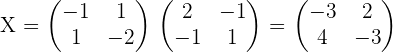
$\text{[math]}$ , this means that there is an inverse $\text{[math]}$

$\text{[math]}$ $\text{[math]}$ $\text{[math]}$

$\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$

$\text{[math]}$

3.Solve the matrix equation:

A · X + 2 · B = 3 · C

$\text{[math]}$

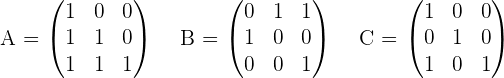
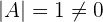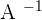
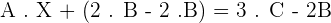
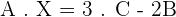
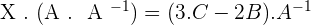
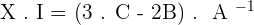
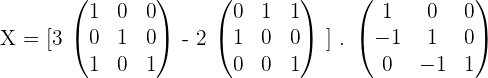
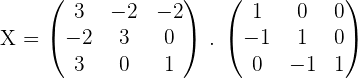
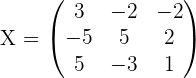
$\text{[math]}$ , this means that there is an inverse $\text{[math]}$

$\text{[math]}$

$\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$

$\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$

4.Solve the matrix equation:

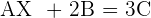
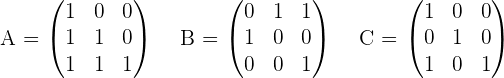
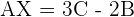
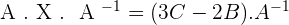
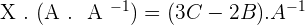
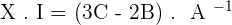
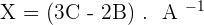
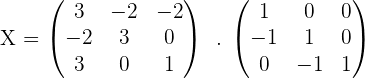
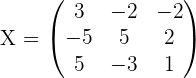
$\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$

$\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$

To solve a system of linear equations, it can be transformed into a matrix equation and then solved.

$\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$

Did you like this article? Rate it!

4.00 (8 rating(s))

Emma

I am passionate about travelling and currently live and work in Paris. I like to spend my time reading, gardening, running, learning languages and exploring new places.

Matrix Equations

Adding Matrices

Matrix Inverse

Types of Matrices

Matrices

Multiplying Matrices

Scalar Matrix Multiplication