Chapters
- Row Matrix
- Column Matrix
- Rectangular Matrix
- Square Matrix
- Zero Matrix
- Upper Triangular Matrix
- Lower Triangular Matrix
- Diagonal Matrix
- Scalar Matrix
- Identity Matrix
- Transpose Matrix
- Regular Matrix
- Singular Matrix
- Idempotent Matrix
- Involutory Matrix
- Symmetric Matrix
- Antisymmetric Matrix
- Orthogonal Matrix
There are many types of matrices but remembering them all can be difficult and that is why we came up with a separate lesson for different types of matrices. When it comes to types of matrix, we look at every point, from rows to their purpose. Following are the types of matrices:
Row Matrix
If a matrix has just one row, we will call it a row matrix. Number of columns doesn't matter in a row matrix, the only thing that matters that it should have a single row. A row matrix is formed by a single row.
Column Matrix
Column matrix is like a row matrix but with some changes. The condition of the column matrix is that it should have a single column. It doesn't matter how many rows are there in a column matrix, the only thing that matters is that it should have a single column.
Rectangular Matrix
A rectangular matrix is formed by a different number of rows and columns, and its dimension is noted as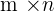 
. Basically, almost all matrices are rectangular matrix but if the rows and columns become the same then it won't be a rectangular matrix.
Square Matrix
When the rows and columns are equal then it won't be a rectangular matrix instead it will be a square matrix. The reason is simple, a square has all equal sides and when the number of rows and columns are equal that means all sides of a matrix are equal hence that is why we call it a square matrix. In short, a square matrix is formed by the same number of rows and columns. The elements of the form 
constitute the principal diagonal. The secondary diagonal is formed by the elements with 
.
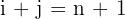Zero Matrix
In a zero matrix, all the elements are zeros.
Upper Triangular Matrix
To understand the upper triangular matrix, make a diagonal of the given matrix. If all the elements below the diagonal are zero that means you have an upper triangular matrix.
Lower Triangular Matrix
Lower triangular matrix is like the upper triangular matrix but the difference is the positioning of zeros. In the lower triangular matrix, all the elements above the diagonal are zero. It doesn't matter what is below the diagonal, as long as the elements above the diagonal are zero, we will call it a lower triangular matrix, however, the diagonal elements will never be zero in both, upper triangular matrix as well as in the lower triangular matrix.
Diagonal Matrix
In a diagonal matrix, all the elements above and below the diagonal are zeros. It is like a combination of an upper triangular matrix and a lower triangular matrix.
Scalar Matrix
A scalar matrix is like a diagonal matrix but with a difference. There are two conditions for the scalar matrix. The first one is that all the elements, above as well as below the diagonal should be zero. The second condition is that the diagonal elements should be the same. Hence, a scalar matrix is a diagonal matrix in which the diagonal elements are equal.
Identity Matrix
An identity matrix is a diagonal matrix in which the diagonal elements are equal to 1.
Transpose Matrix
Given matrix A, the transpose of matrix A is another matrix where the elements in the columns and rows have switched. In other words, the rows become the columns and the columns become the rows.
Regular Matrix
Another name for the regular matrix is non-singular matrix. A regular matrix is a square matrix that has an inverse. In other words, if a square matrix has a non-zero determinant that means it is a regular/non-singular matrix.
Singular Matrix
A singular matrix is a square matrix that has no inverse.
Idempotent Matrix
The matrix A is idempotent if:
Involutory Matrix
The matrix A is involutory if:
An involutory matrix is its own matrix inverse.
Symmetric Matrix
A symmetric matrix is a square matrix that verifies:
Antisymmetric Matrix
An antisymmetric matrix is a square matrix that verifies:
Orthogonal Matrix
A matrix is orthogonal if it verifies that:
Did you like this article? Rate it!
Loading...
