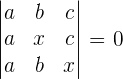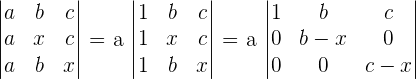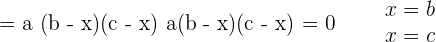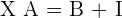Chapters

Exercise 1
Given the matrices:
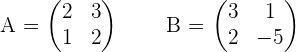
Solve the matrix equation:

Exercise 2
Given the matrices:
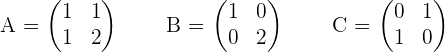
Solve the matrix equation:
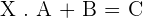
Exercise 3
Given the matrices:

Solve the matrix equations:
Exercise 4
Given the matrices:
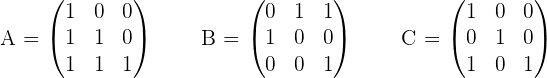
Solve the matrix equation:
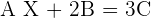
Exercise 5
Solve the matrix equation:

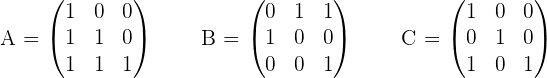
Exercise 6
Solve the system using a matrix equation.

Exercise 7
Calculate A and B:

Exercise 8
Solve the following equations without developing the determinants.
1 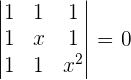
2 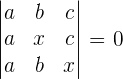
Solution of exercise 1
1Given the matrices:
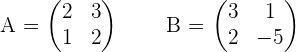
Solve the matrix equation:

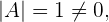 there is the inverse
there is the inverse 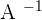
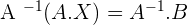

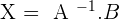

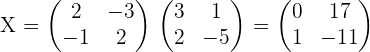
Solution of exercise 2
Given the matrices:
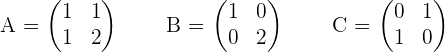
Solve the matrix equation:
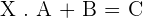
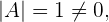 there is the inverse
there is the inverse 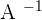
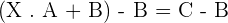

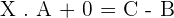

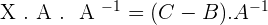
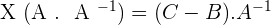
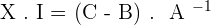

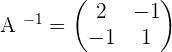


Solution of exercise 3
Given the matrices:

Solve the matrix equations:
1. 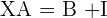


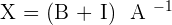

2. 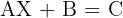
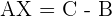




3. 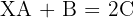
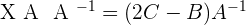
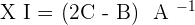
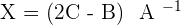
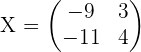
4. 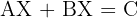

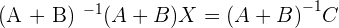
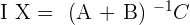

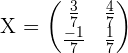
5. 

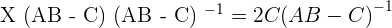


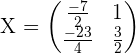
Solution of exercise 4
Given the matrices:
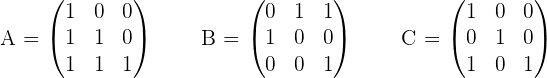
Solve the matrix equation:
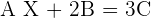
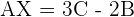

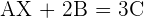




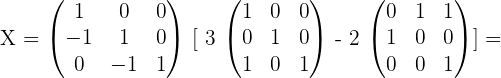

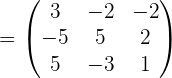
Solution of exercise 5
Solve the matrix equation:

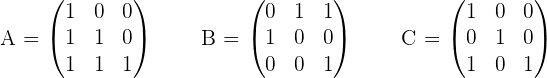
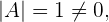

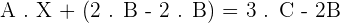
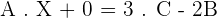
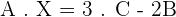
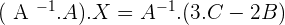


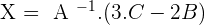

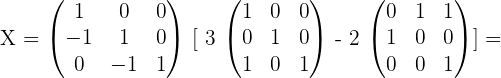

Solution of exercise 6
Solve the system using a matrix equation.

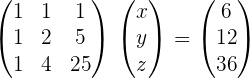
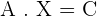



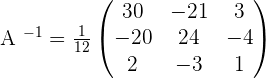
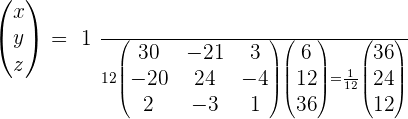

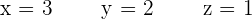
Solution of exercise 7
Calculate A and B:

Multiply the second equation by −2.
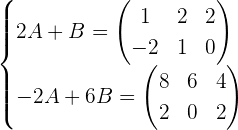
Add the equations.

Multiply the first equation by 3 and add the equations:
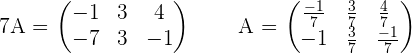
Solution of exercise 8
Solve the following equations without developing the determinants.
1 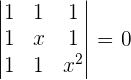




2