Chapters
What is logarithm
Logarithmic and exponential functions are inverses of each other. For example,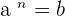 
is an exponential function. In logarithmic form, it can be written as:
A logarithm of a number with the log base e is known as a natural logarithm. It is expressed mathematically as 
or 
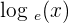. The value of e is equal to 2.71828... The logarithm of a number to the base ten is expressed as 
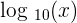and is known as a common logarithm.
Basic Properties of Logarithms
Some of the basic properties of the logarithmic function are as follows:
- The base of the logarithmic function should be greater than 0 and not equal to 1, i.e. in
, 
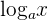and 
. - The base of a logarithm cannot be negative which means it should always be positive
- The logarithm of zero does not exist
- The logarithm of 1 is zero. It can be expressed as
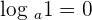, where a is the base of the logarithm - The logarithm with the same base and number is 1. For example, the logarithm of the number b with base b is one. Mathematically it can be expressed as
. For example, we can write the logarithmic function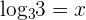 
in exponential form as 
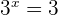. Since, 3 raised to the power 1 is equal to 3, so 
. - If logarithm is in exponential form and base and the number of the logarithm is the same, then it is equal to the value of the exponent. Mathematically it can be expressed as
.
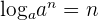Logarithm Rules
When the question involves the term "expand", you need to apply logarithmic rules to simplify the expression and solve for values. Don't find logarithms using a calculator because you are expected to write the answers in whole numbers or fractional form, whereas the calculator will give you a decimal number. Just like rules of exponents, there are different logarithmic rules. These logarithmic rules along with the relevant examples are explained below:
1 Logarithm Product Rule
The logarithm of a product of two numbers is equal to the sum of the logarithm of the numbers. It can be expressed mathematically as:
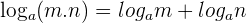
Examples
1 Expand 
According to the logarithm product rule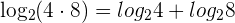 
Suppose,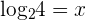 
and 
. Since, logarithm is an inverse function of an exponential equation, so we will rewrite these two logarithms into exponential equations like this:
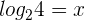
If 2 is raised to a power 2, the answer is 4, i.e.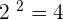 
. Similarly, if 2 is raised the power 3, the answer is 8, i.e. 
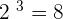. Hence, the values for 
and 
are 2 and 3 respectively. Hence, the final answer is:
= 
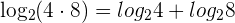
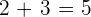
2 Expand 
According to the logarithm product rule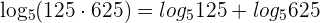 
Suppose, 
and 
. Write these two logarithmic functions in exponential forms like this:
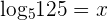
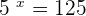
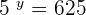
If 5 is raised to the power 3, the answer is 125, i.e.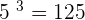 
. Similarly, if 5 is raised the power 4, the answer is 625, i.e. 
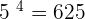. Hence, the values for and are 3 and 4 respectively. Hence, the final answer is:
= 
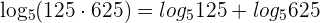
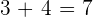
2 Logarithm Quotient Rule
The logarithm of division of m and n is equal to the difference of logarithm of m and logarithm of n. Remember that the rule is true for the logarithm of numerator - logarithm of denominator, not the other way around. Mathematically, it can be expressed as:
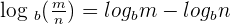
Examples
1 Expand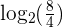 
According to the logarithm quotient rule,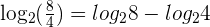 
. Suppose 
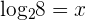and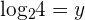 
. Write these two logarithmic functions in exponential forms like this:
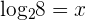
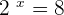
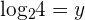
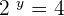
We know that when 2 raised to the power 3 is equal to 8, i.e. 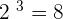and 2 raised to the power 2 is equal to 4, i.e. 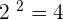. Hence, the final answer will be:
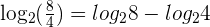
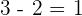
2 Expand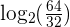 
According to the logarithm quotient rule,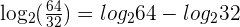 
. Suppose 
and 
. Write these two logarithmic functions in exponential forms like this:
We know that 2 raised to the power 6 is equal to 64, i.e.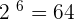 
and 2 raised to the power 5 is equal to 32, i.e. 
. Hence, the final answer will be:
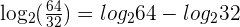
Remember that the logarithm product and quotient rules are only applicable to the function having the same base. For example, from the above examples you can conclude that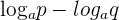 
can be written as a single logarithmic function as 
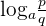. The expressions 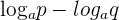are combined to form a single expression 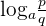because they had a common base a. We cannot combine 
into a single expression because both the logarithmic functions have different bases a and b. The same rule applies to the logarithm product rule.
3 Logarithm Power Rule
The logarithm of the power is equal to the product of the power or exponent and the logarithm of the number. It can be expressed mathematically as:
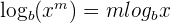
Examples
1 Expand 
According to the logarithm power rule,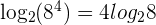 
Suppose 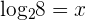. First, we will convert 
into exponential form like this:
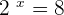
We know that 2 raised to the power 3 is equal to 8, i.e. 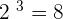, so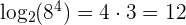 
.
2 Expand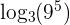 
According to the logarithm power rule,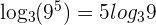 
Suppose 
. First, we will convert 
into exponential form like this:
We know that 3 raised to the power 2 is equal to 9, i.e.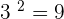 
, so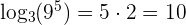 
.
4 Logarithm Base Switch Rule
The base a of logarithmic function b is equal to the reciprocal of logarithm a with base b. It can be expressed mathematically as:
Examples
1 Prove 
Let us solve left hand side of the above expression first.
Suppose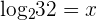 
.
By converting the above log form into the exponential notation we get the following expression:
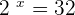
Since, 2 to the power 5 is equal to 32, i.e. 
, so 
Now, we will solve right hand side of the above expression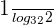 
Suppose 
. When we will write it in exponential form, we will get the following expression:
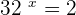
We know that 2 raised to the power 5 is equal to 32. Hence, we can say that 32 raised to the power 
is equal to 2. Hence,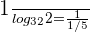 
which is equal to 5.
2 Prove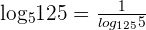 
Lets solve left hand side of the above expression first.
Suppose .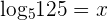
Writing it in exponential notation we get the following expression:
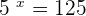
Since, 5 to the power 3 is equal to 125, i.e. 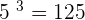, so 
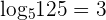
Now, we will solve right hand side of the above expression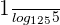 
Suppose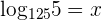 
. When we will write it in exponential form, we will get the following expression:
We know that 5 raised to the power 3 is equal to 125. Hence, we can say that 125 raised to the power 
is equal to 5. Hence, 
which is equal to 3. Hence, this logarithmic rule is proved because left hand side is equal to the right hand side.
You could check for reputable maths tutors here.
5 Logarithm Root Rule
The logarithm of a root is equal to the product between the logarithm of the radicand and the index of the root. It can be expressed mathematically as:
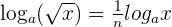
Examples
1 Expand 
According to the logarithm root rule, 
. Suppose 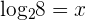. Convert this logarithmic expression into the exponential form like this:
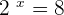
We know that 2 raised to the power 3 is equal to 8, i.e. .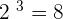
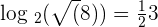
2 Expand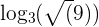 
According to the logarithm root rule,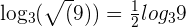 
. Suppose . Convert this logarithmic expression into the exponential form like this:
We know that 3 raised to the power 2 is equal to 9, i.e. 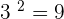. It means that 
.
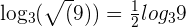
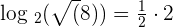
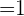
6 Change of Base
This logarithmic rule can be described mathematically as:
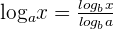
Examples
1 Prove 
First solve left hand side of the expression first by converting it into the exponential form:
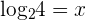
Since, 2 raised to the power 2 is equal to 4, hence the value of x is equal to 2. Now, we will solve right hand side of the equality 
. Suppose 
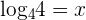and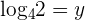 
. Convert these logarithmic functions into exponential forms to find their values:
and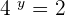 
We know that 4 raised to the power 1 is equal to 4, so 
. Similarly, 4 raised to the power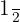 
is equal to 2, so 
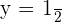. Put these values in the expression 
.
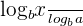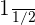
Hence, the logarithmic rule is proved through this example because the left hand side is equal to the right-hand side.
2 Prove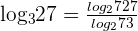 
First solve left hand side of the expression first by converting it into the exponential form:
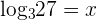
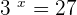
Since 3 raised to the power 3 is equal to 27, hence the value of is equal to 3. Now, we will solve right hand side of the logarithmic equation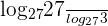 
. Suppose 
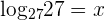and 
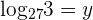. Convert these logarithmic functions into exponential forms to find their values:
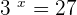and 
We know that 3 raised to the power 3 is equal to 27, so . Similarly, 27 raised to the power is equal to 3, so 
. Put these values in the right hand side of the logarithmic equation .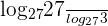
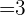
Hence, the left hand side of the logarithmic equation is equal to the right-hand side, so this rule is proved.
Did you like this article? Rate it!
Loading...
