Exercise 1
A company manufactures and sells two models of lamps, L1 and L2. To manufacture each lamp, the manual work involved in model L1 is 20 minutes and for L2, 30 minutes. The mechanical (machine) work involved for L1 is 20 minutes and for L2, 10 minutes. The manual work available per month is 100 hours and the machine is limited to only 80 hours per month. Knowing that the profit per unit is 
10 for L1 and L2, respectively, determine the quantities of each lamp that should be manufactured to obtain the maximum benefit.
Exercise 2
With the start of school approaching, a store is planning on having a sale on school materials. They have 600 notebooks, 500 folders and 400 pens in stock, and they plan on packing it in two different forms. In the first package, there will be 2 notebooks, 1 folder and 2 pens, and in the second one, 3 notebooks, 1 folder and 1 pen. The price of each package will be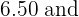 
7.00 respectively. How many packages should they put together of each type to obtain the maximum benefit?
Exercise 3
On a chicken farm, the poultry is given a healthy diet to gain weight. The chickens have to consume a minimum of 15 units of Substance A and another 15 units of Substance B. In the market there are only two classes of compounds: Type X, with a composition of one unit of A to five units of B, and another type, Y, with a composition of five units of A to one of B. The price of Type X is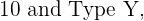 
30. What are the quantities of each type of compound that have to be purchased to cover the needs of the diet with a minimal cost?
Exercise 4
There is only 600 milograms of a certain drug that is needed to make both large and small pills for small scale pharmaceutical distribution. The large tablets weigh 40 milograms and the small ones, 30 milograms. Consumer research determines that at least twice the amount of the smaller tablets are needed than the large ones and there needs to be least three large tablets made. Each large tablet is sold for a profit of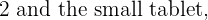 
1. How many tablets of each type have to be prepared to obtain the maximum profit?
Solution of exercise 1
A company manufactures and sells two models of lamps, L1 and L2. To manufacture each lamp, the manual work involved in model L1 is 20 minutes and for L2, 30 minutes. The mechanical (machine) work involved for L1 is 20 minutes and for L2, 10 minutes. The manual work available per month is 100 hours and the machine is limited to only 80 hours per month. Knowing that the profit per unit is 10 for L1 and L2, respectively, determine the quantities of each lamp that should be manufactured to obtain the maximum benefit.
Step 1 - Identify the decision variables
x = number of lamps L1
y = number of lamps L2
Step 2 - Write the objective function
Write the objective function.
Step 3 - Write the set of constraints
Write the constraints as a system of inequalities.
Convert the time from minutes to hours.
20 min = 1/3 h
30 min = 1/2 h
10 min = 1/6 h
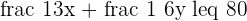
As the number of lamps are natural numbers, there are two more constraints:
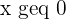
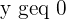
Step 4 - Choose the method to solve the problem
We will solve this problem graphically.
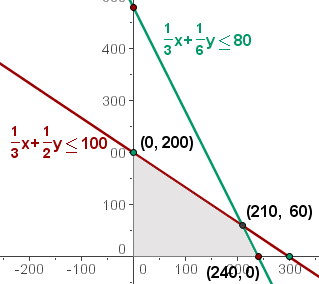
Step 5 - Construct the graph
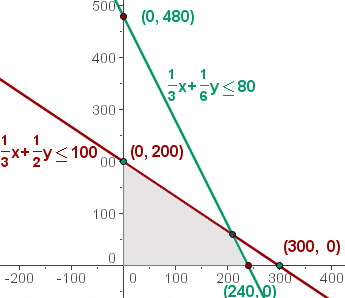
Find the set of feasible solutions that graphically represent the constraints.
Represent the constraints graphically.
As 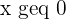and 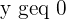, work in the first quadrant.
Solve the inequality graphically:
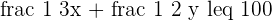
Take a point on the plane, for example (0,0).
Step 6 - Find the feasibility region of the graph
The area of intersection of the solutions of the inequalities would be the solution to the system of inequalities, which is the set of feasible solutions.
Step 7 - Find the optimum point
Calculate the coordinates of the vertices from the compound of feasible solutions.
The optimal solution, if unique, is a vertex. These are the solutions to systems:
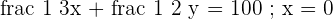
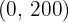
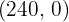
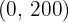
Calculate the value of the objective function at each of the vertices to determine which of them has the maximum or minimum values.
In the objective function, place each of the vertices that were determined in the previous step.
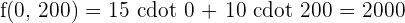
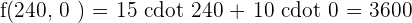
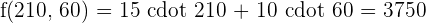Maximum
The optimum solution is to manufacture 210 units of model L1 and 60 units of model L1 to obtain a benefit of 
6.50 and 
f(x, y) = 6.5x + 7y
x + y leq 500
2x + 3y leq 6002x + y leq 400x geq 0y geq 0
f(x,y) = 6.5 cdot 200 + 7 cdot 0 = 1300f(x,y) = 6.5 cdot 0 + 7 cdot 200 = 1400f(x,y) = 6.5 cdot 150 + 7 cdot 100 = 1675
1675.
Solution of exercise 3
On a chicken farm, the poultry is given a healthy diet to gain weight. The chickens have to consume a minimum of 15 units of Substance A and another 15 units of Substance B. In the market there are only two classes of compounds: Type X, with a composition of one unit of A to five units of B, and another type, Y, with a composition of five units of A to one of B. The price of Type X is 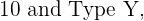30. What are the quantities of each type of compound that have to be purchased to cover the needs of the diet with a minimal cost?
Step 1 - Identify the decision variables
x = X
y = Y
Step 2 - Write the objective function.
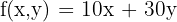
Step 3 - Identify the constraints
Write the constraints as a system of inequalities.
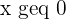
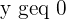
Step 4 - Choose the method to solve the problem
We will solve this problem graphically.
Step 5 - Construct the graph
Step 6 - Find the feasibility region
Find the set of feasible solutions that graphically represent the constraints.
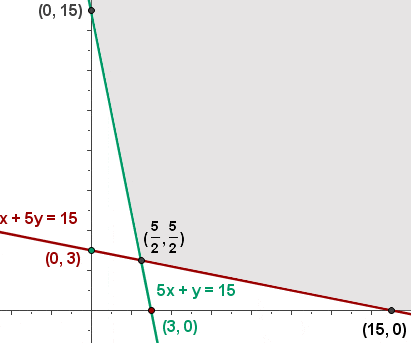
The grey highlighted area represents the feasibility region.
Step 7 - Find the optimum point
Calculate the coordinates of the vertices from the compound of feasible solutions.
Calculate the value of the objective function at each of the vertices to determine which of them has the maximum or minimum values. It must be taken into account the possible non-existence of a solution if the compound is not bounded.
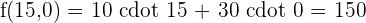
Minimum
The minimum cost is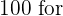 
X = frac {5} {2} 
Y = frac{5}{2}
2 and the small tablet, 
f(x, y) = 2x + y
40x + 30y leq 600x geq 3y geq 2xx geq 0y geq 0
f(x,y) = 2 cdot 3 + 16 = 22f(x,y) = 2 cdot 3 + 6 = 12f(x,y) = 2 cdot 6 + 12 = 24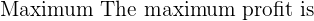
24, and is obtained by making 6 units of the large tablets and 12 units of the small tablets.
Did you like this article? Rate it!
Loading...
An agricultural Research institute suggested to a farmer to spread out at least 4800kg of a special phosphate fertilizer and not less than 7200kg of a special nitrogen fertilizer to raise productivity of crops in his fields. There are two sources for obtaining these: Mixture A and B, both of these are available in bags weighting 100 kg each and they cost sh 40 and sh24 respectively. Mixture A contains phosphate and nitrogen equivalent of 20 kg and 80 kg respectively, while mixture B contains these ingredients equivalent of 50 kg each.
Required: Write this as a linear programming problem and determine how many bags of each type the farmer should buy in order to obtain the required fertilizer at a minimum cost
Very good
Please help to do under this question
A company produces two types of TVs, one of which is black and white, the
other colour. The company has the resources to make at most 200 sets a week. Creating a black
and white set includes Birr 2700 and Birr 3600 to create a colored set. The business should
spend no more than Birr 648,000 a week producing TV sets. If it benefits from Birr 525 per set
of black and white and Birr 675 per set of colours.
Construct the linear programing model.
How many sets of black/white and colored sets it should produce in order to get
maximum profit using
Graphical Method and Simplex Method
A company manufacture two types of product A1 and A2. Each product using milling and drilling machine. The process time per unit of A1 on the milling is 10 hours and the drilling is 8 hours, the process time per unit of A2 on the milling is 15 minute and on the drilling is 10 hours, the maximum number of hours available per week on the drilling and milling machine are 80 hours and 60 hours respectively also the profit per selling of A1 and A2 are 25 naira and 35 naira respectively. Formulate a LP model to determine the production volume of each of the product such that the total profit is maximized
so this equestion of linear programming what have a solution
A linear programming problem
Please help to do this qutions,
Ethio Manufacturing, a renowned company in Ethiopia, specializes in
producing two types of products: Product A and Product B, with the primary
objective of maximizing its total profit. Each unit of Product A yields a profit
of 5 Birr, and each unit of Product B yields a profit of 4 Birr.
The company is
constrained by limited resources in two vital departments: Department A, with 60 hours of available production time, where producing one unit of
Product A consumes 3 hours and one unit of Product B consumes 2 hours;
and Department B, with 72 hours of available production time, where
producing one unit of Product A takes 4 hours and one unit of Product B
takes 3 hours. Questions
1. Formulate the Linear Programming Problem (LPP):
2.Graphically analyze the LPP to determine the optimal production quantities
of Product A and Product B that maximize Ethio Manufacturing’s profit. Identify the coordinates of the optimal solution point.
3. Apply the simplex method to find the optimal solution for Ethio
Manufacturing’s LPP. Present the initial tableau, pivot steps, and the final
solution. Explain each step in the simplex method.
4. Determine the dual problem for Ethio Manufacturing’s LPP and present
the dual problem’s objective function and constraints.
5a. Discuss the changes in objective-function coefficients (cj) of the optimal basic feasible solution
5b. Discuss the effect of discrete change in the avaliabilty of resources from
[60, 72 ]T to [70, 50]T
Hi pls hw d u obtain d constraints in for truck type B in exercise 1