Chapters
Optimization of resources (cost and time) is required in every aspect of our lives. We need the optimization because we have limited time and cost resources, and we need to take the maximum out of them. Every aspect of the business world today requires optimization, from manufacturing to resolving supply chain issues to stay competitive.
Linear programming offers the easiest way to do optimization as it simplifies the constraints and helps to reach a viable solution to a complex problem. In this article, we will solve some of the linear programming problems through the graphing method.
Exercise 1
A transport company has two types of trucks, Type A and Type B. Type A has a refrigerated capacity of 
and a non-refrigerated capacity of 
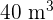. In contrast, Type B has the same overall volume with equal refrigerated and non-refrigerated stock sections. A grocer must hire trucks to transport 
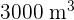of refrigerated stock and 
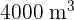of non-refrigerated stock. The cost per kilometre of Type A is 
, and 
for Type B. How many trucks of each type should the grocer rent to achieve the minimum total cost?
Exercise 2
A school is preparing a trip for 400 students. The transportation company has 10 buses of 50 seats each and 8 buses of 40 seats but only has 9 drivers available. The rental cost for a large bus is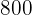 
and 
for a small bus. Calculate how many buses of each type should be used for the trip for the least possible cost.
Exercise 3
A store wants to liquidate 200 shirts and 100 pairs of pants from last season. They have decided to put together two offers, A and B. Offer A is a package of one shirt and a couple of pants which will sell for . Offer B is a package of three shirts and a pair of pants, which will sell for 
. The store does not want to sell less than 20 packages of Offer A and less than 10 of Offer B. How many boxes do they have to deal with to maximize the money generated from the promotion?
Solution of Exercise 1
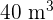A transport company has two types of trucks, Type A and Type B. Type A has a refrigerated capacity of and a non-refrigerated capacity of . In contrast, Type B has the same overall volume with equal refrigerated and non-refrigerated stock sections. A grocer must hire trucks to transport 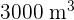of refrigerated stock and 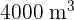of non-refrigerated stock. The cost per kilometre of Type A is , and for Type B. How many trucks of each type should the grocer rent to achieve the minimum total cost?
a) Choose the unknowns.
x = Type A trucks
y = Type B trucks
b) Write the objective function.
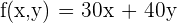
c) Write the constraints as a system of inequalities.
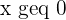
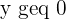
d) Find the set of feasible solutions that graphically represent the constraints.
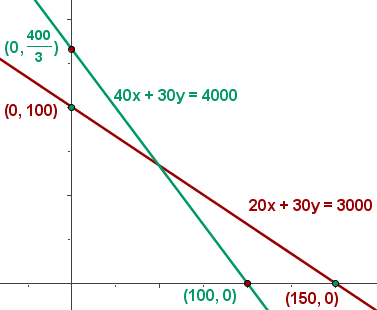
e) Calculate the coordinates of the vertices from the compound of feasible solutions.
f) Calculate the value of the objective function at each vertex to determine which has the maximum or minimum values.
As x and y must be natural numbers round the value of y.
By default, we see what takes the value x to y = 66 in the equation 
, which is within the feasible solutions.
The minimum cost is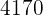 
. To achieve this 51 trucks of Type A and 66 trucks of Type B are needed.
Solution of exercise 2
A school is preparing a trip for 400 students. The company who is providing the transportation has 10 buses of 50 seats each and 8 buses of 40 seats, but only has 9 drivers available. The rental cost for a large bus is 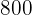and for a small bus. Calculate how many buses of each type should be used for the trip for the least possible cost.
a)Choose the unknowns.
x = small buses
y = big buses
b) Write the objective function.
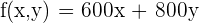
c) Write the constraints as a system of inequalities.
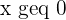
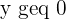
d) Find the set of feasible solutions that graphically represent the constraints.
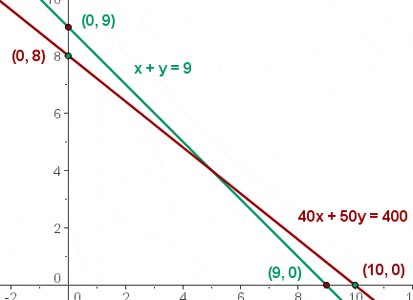
e) Calculate the coordinates of the vertices from the compound of feasible solutions.
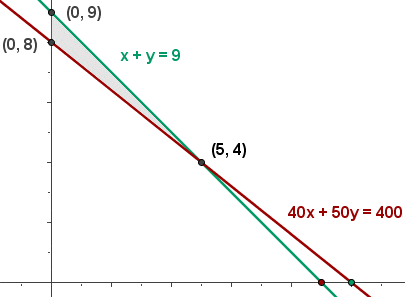
Example 2 - part e
f) Calculate the value of the objective function at each vertex to determine which has the maximum or minimum values.
Hence, the minimum cost is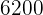 
. This is achieved with 4 large and 5 small buses.
We substituted the points (0,9), (0,8), and (5,4) in the equation to determine the minimum cost. However, you can tell this by directly looking at the graph. The coordinate (5,4) comes under the feasible region and is the minimum point of it.
Solution of exercise 3
A store wants to liquidate 200 shirts and 100 pairs of pants from last season. They have decided to put together two offers, A and B. Offer A is a package of one shirt and a pair of pants which will sell for . Offer B is a package of three shirts and a pair of pants, which will sell for . The store does not want to sell less than 20 packages of Offer A and less than 10 of Offer B. How many packages of each do they have to deal to maximize the money generated from the promotion?
a) Choose the unknowns.
x = number of packages of Offer A
y = number of packages of Offer B
b) Write the objective function.
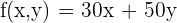
c) Write the constraints as a system of inequalities.
d) Find the set of feasible solutions that graphically represent the constraints.
Example 3 - part d
e) Calculate the coordinates of the vertices from the compound of feasible solutions.
Example 3 - part e
f) Calculate the value of the objective function at each vertices to determine which has the maximum or minimum values.
50 packages of each offer generate a maximum of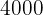 
in sales.
Did you like this article? Rate it!
Loading...
An agricultural Research institute suggested to a farmer to spread out at least 4800kg of a special phosphate fertilizer and not less than 7200kg of a special nitrogen fertilizer to raise productivity of crops in his fields. There are two sources for obtaining these: Mixture A and B, both of these are available in bags weighting 100 kg each and they cost sh 40 and sh24 respectively. Mixture A contains phosphate and nitrogen equivalent of 20 kg and 80 kg respectively, while mixture B contains these ingredients equivalent of 50 kg each.
Required: Write this as a linear programming problem and determine how many bags of each type the farmer should buy in order to obtain the required fertilizer at a minimum cost
Very good
Please help to do under this question
A company produces two types of TVs, one of which is black and white, the
other colour. The company has the resources to make at most 200 sets a week. Creating a black
and white set includes Birr 2700 and Birr 3600 to create a colored set. The business should
spend no more than Birr 648,000 a week producing TV sets. If it benefits from Birr 525 per set
of black and white and Birr 675 per set of colours.
Construct the linear programing model.
How many sets of black/white and colored sets it should produce in order to get
maximum profit using
Graphical Method and Simplex Method
A company manufacture two types of product A1 and A2. Each product using milling and drilling machine. The process time per unit of A1 on the milling is 10 hours and the drilling is 8 hours, the process time per unit of A2 on the milling is 15 minute and on the drilling is 10 hours, the maximum number of hours available per week on the drilling and milling machine are 80 hours and 60 hours respectively also the profit per selling of A1 and A2 are 25 naira and 35 naira respectively. Formulate a LP model to determine the production volume of each of the product such that the total profit is maximized
so this equestion of linear programming what have a solution
A linear programming problem
Please help to do this qutions,
Ethio Manufacturing, a renowned company in Ethiopia, specializes in
producing two types of products: Product A and Product B, with the primary
objective of maximizing its total profit. Each unit of Product A yields a profit
of 5 Birr, and each unit of Product B yields a profit of 4 Birr.
The company is
constrained by limited resources in two vital departments: Department A, with 60 hours of available production time, where producing one unit of
Product A consumes 3 hours and one unit of Product B consumes 2 hours;
and Department B, with 72 hours of available production time, where
producing one unit of Product A takes 4 hours and one unit of Product B
takes 3 hours. Questions
1. Formulate the Linear Programming Problem (LPP):
2.Graphically analyze the LPP to determine the optimal production quantities
of Product A and Product B that maximize Ethio Manufacturing’s profit. Identify the coordinates of the optimal solution point.
3. Apply the simplex method to find the optimal solution for Ethio
Manufacturing’s LPP. Present the initial tableau, pivot steps, and the final
solution. Explain each step in the simplex method.
4. Determine the dual problem for Ethio Manufacturing’s LPP and present
the dual problem’s objective function and constraints.
5a. Discuss the changes in objective-function coefficients (cj) of the optimal basic feasible solution
5b. Discuss the effect of discrete change in the avaliabilty of resources from
[60, 72 ]T to [70, 50]T
Hi pls hw d u obtain d constraints in for truck type B in exercise 1