Chapters
Introduction
Linear programming is a technique to obtain the best result in the mathematical model. The essentials of the mathematical model are depicted by the linear relationships. In other words, it is a response to situations that require the maximization or minimization of certain functions which are subject to limitations. These limitations are called constraints.
Applications of Linear Programming
The applications of linear programming for optimization in certain fields are widespread. In manufacturing industry, it can be utilized to determine how to allocate labor and resources to maximize the profits, and minimize the cost of operations. It can also be used to determine which products should be sold in which specific quantity to maximize the earnings. In logistics, it tells us how to allocate the resources so that we can achieve more in less time. In operations research, we can express practical problems as linear programming problems. Linear programming was widely used in preliminary development of microeconomics.
Today, it is widely used in management science as the companies utilize it for managing the company's operations such as planning , production, technology, and transportation. The primary goal of the businesses are to maximize the profits, and minimize the costs. Hence, certain issues can be expressed as linear programming problems to reach a viable conclusion.
Objective Function
We know that the linear programming optimizes a system of linear constraints and a linear objective function. You may be wondering what is a linear objective function. Well, this function elucidate the quantity that needs optimization. The main objective of the linear programming is to fetch the values of variables that minimize or maximize the objective function. Hence, we can say that linear programming optimizes (maximize or minimize) an objective function (a linear function of several variables):
Constraints
The objective function is subject to certain constraints, expressed by linear inequalities. These constraints are actually the limitations on the primary decision variables.
 | a1x + b1y ≤ c1 |
| a2x + b2y ≤c2 | |
| ... ... ... | |
| anx + bny ≤cn |
Each inequality constraint system determines a half-plane.
Feasible Solution
The feasibility region of the linear programming problem shows set of all feasible solutions. A feasible solution of the linear programming problem satisfies every constraint of the problem.
Optimal Solution
It is also included in the feasible region, however it represents the maximum objective value of the function for the problem which requires maximization and smallest objective value of the function that requires minimization.
There are many methods to solve linear programming problems. These methods include a simplex method, graphing method, northwest corner method, and least cost method. In this article, we will see how to solve these problems using the graphing method. You must know how to graph a system of linear inequalities and highlight their overlapping region to determine the solutions.
Example 1
A furniture company produces office chairs and tables. The company projects the demand of at least 100 chairs and 50 tables daily. The company can produce no more than 120 chairs and 70 tables daily. The company must ship at most 150 units of chairs and tables daily to fulfill the shipping contract.
Each sold table results in the profit of 
15 profit.
a) How many units of chairs and tables should be made daily to maximize the profit?
b) Compute the maximum profit the company can earn in a day?
Solution
Part a
We will start to solve the above optimization problem by defining the variables first.
Suppose:
The number of chairs sold daily = x
The number of tables sold daily = y
The equation will be written as:
Now, the next step will be to define the constraints.
It is given in the problem that there is a projected demand for at least 100 chairs daily and the company cannot produce more than 150 chairs. Hence, we will write this constraint as an inequality like this:
The problem says that there is a projected demand for at least 50 tables daily and the company cannot produce more than 70 tables. Hence, we will write this constraint as an inequality like this:
To satisfy the shipping contract, the company must ship at most 15o units of both chairs and tables daily. We will write this constraint as:
We will graph the following inequalities in an xy plane:
We will graph these inequalities in an xy plane like this:
You can see that at point (100,50), all the three lines of the graph are intersecting each other. There only one feasible solution which is also the optimal solution of the problem. The point (100,50) satisfies all the constraints of the problem. Hence, to optimize the profits, the company must make 100 chairs and 50 table daily.
Part b
The maximum profit can be computed by putting x = 100 and y = 50 in the following equation,
4000
320 by selling each business class ticket and a profit of 
320 for each business class ticket and a profit of 
P = 320x + 400y
xgeq 25
y geq 90
x + y leq 180
x + y leq 180xgeq 25y geq 90
P = 320x + 400y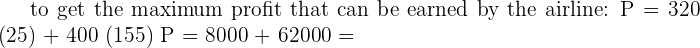
70000
Did you like this article? Rate it!
Loading...
A travel agent is organizing a trip for a professional body. She can make arrangements for maximum of 10 people and least four men and three woman in the group . Hee profit is$12.25 fpr each woman and $15.40 for each group.
Solve the linear programming problem using graphical method
I very much appreciate the exercises and solutions however, it seems that the answer to the third exercise has an issue. A couple of jeans refers to two pairs not one so the equation x + y = 100 is supposed to be 2x+ y = 100. Perhaps there was an issue with the wording because I just realized it is a pair in the solution but a couple in the question
I really don’t understand this thing well
Where is 3 coming from in solution exercise 3
An agricultural Research institute suggested to a farmer to spread out at least 4800kg of a special phosphate fertilizer and not less than 7200kg of a special nitrogen fertilizer to raise productivity of crops in his fields. There are two sources for obtaining these: Mixture A and B, both of these are available in bags weighting 100 kg each and they cost sh 40 and sh24 respectively. Mixture A contains phosphate and nitrogen equivalent of 20 kg and 80 kg respectively, while mixture B contains these ingredients equivalent of 50 kg each.
Required: Write this as a linear programming problem and determine how many bags of each type the farmer should buy in order to obtain the required fertilizer at a minimum cost
Very good
Please help to do under this question
A company produces two types of TVs, one of which is black and white, the
other colour. The company has the resources to make at most 200 sets a week. Creating a black
and white set includes Birr 2700 and Birr 3600 to create a colored set. The business should
spend no more than Birr 648,000 a week producing TV sets. If it benefits from Birr 525 per set
of black and white and Birr 675 per set of colours.
Construct the linear programing model.
How many sets of black/white and colored sets it should produce in order to get
maximum profit using
Graphical Method and Simplex Method