Chapters

Types of System of Linear Inequalities
A set of two or more linear inequalities form a system of linear inequalities.
There are two types of systems of linear inequalities:
- System of linear inequalities in one variable
- System of linear inequalities in two variables
System of linear inequalities in one variable is represented on the number line, whereas the system of linear inequalities in two variables is graphed on a coordinate axis. In this article, we will find solution set of system of linear inequalities in two variables.
How System of Linear Equations are Solved
We know that system of linear equations are solved using one of the three methods - substitution, elimination and graphing. Systems of equations can be solved easily without graphing through substitution method or elimination. However, inequalities in systems of linear inequalities may have different signs so finding solution set through graphing is sometimes the only, and most of the time the best option.
Number of Solutions in Systems of Linear Inequalities
System of inequalities may have zero, one or many solutions. Zero solution means there is not a single ordered pair which satisfies both the inequalities. One solution means only one ordered pair (x,y) falls in the solution area of the graph. Many solutions means more than one ordered pairs (x,y) fall in the solution area of the graph. System of linear inequalities in two variables contains two linear inequalities in the same system. In this article, we will see how to solve system of linear inequalities in two variables through examples.
Example 1
Find the solution set of the following system of linear inequalities in two variables.
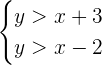
Solution
Follow the following step by step procedure to solve the above system of inequalities.
Step 1- Graph the first inequality 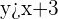
First, graph the inequality 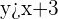 . To graph the inequality we need to construct a table of
. To graph the inequality we need to construct a table of  and
and  values first.
values first.
| x | y |
|---|---|
| -1 | 2 |
| 0 | 3 |
| 1 | 4 |
| 2 | 5 |
| 3 | 6 |
We will construct the graph by plotting the values from the table in the coordinate plane like equations. Since, the inequality is strict, i.e. it has greater than sign, therefore we will use a dashed line to represent it on the coordinate axis. The graph of the inequality 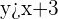 will look like this:
will look like this:

You can see that as the inequality had greater than sign, so we will represent its sign by shading the region above the dashed line.
Step 2-Graph the second inequality 
Now, graph the second inequality  . But to graph, we need to first construct the table of
. But to graph, we need to first construct the table of  and
and  values.
values.
| x | y |
|---|---|
| -2 | -4 |
| -1 | -3 |
| 0 | -2 |
| 1 | -1 |
| 2 | 0 |
Construct the graph using the above table. Again, as the inequality is strict, so we will use a dotted line to represent it.
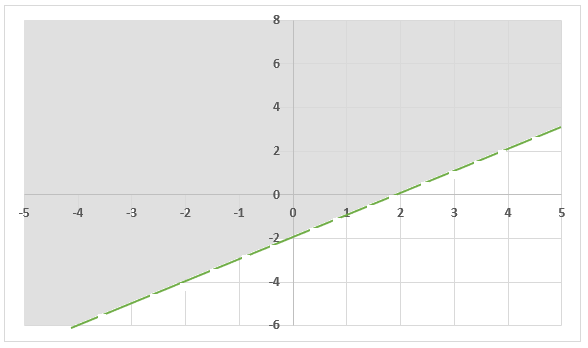
Step 3-Shade the solution area
Construct the graphs of both inequalities in a single plane and highlight the solution.

The solution part of the graph is shaded in light blue color. You can see that the graphs of both the inequalities are parallel. If we were solving system of equations and the graph was parallel, then it would have meant that the system of equations have no solution. But this does not apply to system of inequalities because they have greater than, smaller than, greater than equal to, and less than equal to signs. Their solution lies above or below the straight line, unlike systems of equation whose solutions strictly lie on the straight line.
Step 4-Verify the solution set by substitution
Now, we will take some ordered pairs from the solution region and see whether they satisfy both the inequalities. You can see from the shaded region in the above graph that (1,6) and (-2,4) are part of the solution.
First, substitute (1,6) in both the inequalities like this:
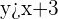

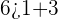

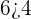
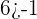
Hence, the ordered pair (1,6) is true for both the inequalities.
Similarly, test the ordered pair (-2,4) like this:
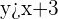

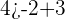

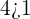
You can also take other ordered pairs in the shaded area and check them by substituting in the inequalities.
Example 2
Find the solution set of the following system of linear inequalities in two variables.
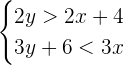
Find various Maths tutor on Superprof.
Solution
Follow the following step by step solution to solve the above system of inequalities. Since, the above system of inequalities are not in the slope intercept form, so we will first convert them into this form by isolating the variable  on the left hand side of the inequality.
on the left hand side of the inequality.
Step 1- Convert the inequality  into slope intercept form
into slope intercept form
Slope intercept form of the linear equations is  . Convert the inequality into slope intercept form of linear functions algebraically. To isolate the variable
. Convert the inequality into slope intercept form of linear functions algebraically. To isolate the variable  on the left hand side, both sides of the inequality will be divided by 2.
on the left hand side, both sides of the inequality will be divided by 2.
Step 2 - Graph the inequality 
For graphing the inequality, we will first construct a table.
| x | y |
|---|---|
| -2 | 0 |
| -1 | 1 |
| 0 | 2 |
| 1 | 3 |
| 2 | 4 |
| 3 | 5 |
Now, plotting these values we will construct a graph like this:

The shaded region above the dashed line represent the solution of the inequality.
Step 3-Convert the second inequality 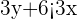 into slope intercept form
into slope intercept form
To convert it into slope intercept form divide both sides by 3
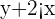
Subtract 2 from both sides of the inequality to get the inequality in slope intercept form:
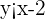
Step 4- Graph the inequality 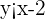
To graph the inequality, first, you need to construct a table like this:
| x | y |
|---|---|
| -2 | -4 |
| -1 | -3 |
| 0 | -2 |
| 1 | -1 |
| 2 | 0 |
| 3 | 1 |
Using the values from the table, construct a graph like this:

As the inequality has less than sign, so we have shaded the region below the dashed line.
Step 5 - Plot the system of equations and shade the solution region
There is no region on the coordinate axis which is overlapped by both the inequalities. Hence, the system of inequality has no solution. The below graph shows this situation:
You can see that no region is shaded because there is no solution.
Example 3
Find the solution set of the following system of linear inequalities in two variables.
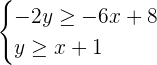
Solution
First we will simplify the above inequalities and then graph them to find the solution set.
Step 1- Simplify the inequality 
Divide both sides of the inequality by -2 to isolate  on the left hand side of the inequality:
on the left hand side of the inequality:

We know that when both sides of the inequality are multiplied or divide by a negative number, the sign of the inequality flips. In the above inequality greater than or equal to sign has changed to less than or equal to.
Step 2- Graph the inequality 
To graph the inequality, first, we need to create a table of  and
and  values like this:
values like this:
| x | y |
|---|---|
| -2 | -10 |
| -1 | -7 |
| 0 | -4 |
| 1 | -1 |
| 2 | 2 |
Now, plot these values on the coordinate axis to get a graph like this.

You can see that a solid straight line is used to graph this inequality because the inequality sign was less than or equal to.
Step 3- Graph the second inequality 
To graph the inequality, first, you need to construct a table like this:
| x | y |
|---|---|
| -2 | -1 |
| -1 | 0 |
| 0 | 1 |
| 1 | 2 |
| 2 | 3 |
Plot these values to get the following graph:
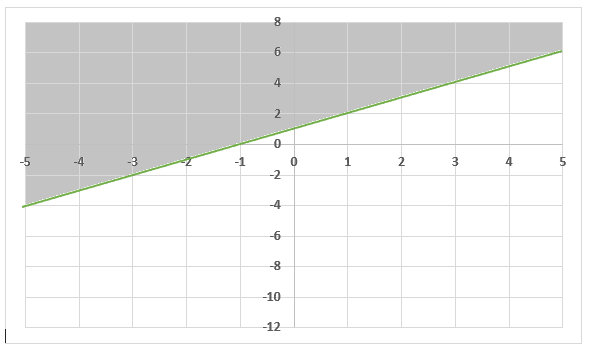
Again, we have used a solid line and shaded the region above the line to represent the greater than equal to sign.
Step 4 - Graph the system of inequalities and shade the solution area
Now, the next step is to graph both the inequalities in the same coordinate axis and shade the solution region.
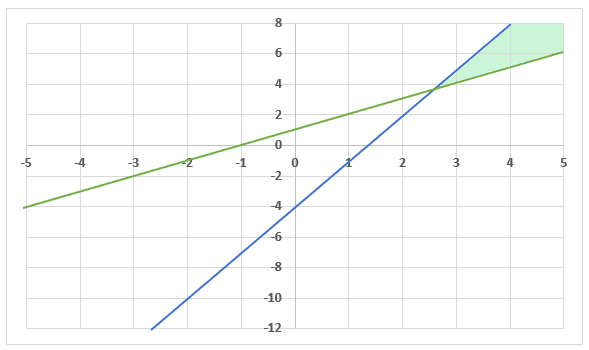
The solution area is shaded in the above graph. It is the area where the solution of the system of inequalities lies.
Step 5 - Verify the solution set by substitution
Now, take ordered pairs in the solution region and verify by substituting them in the system of inequalities.
Suppose we take (4,5) and (5,6). Let us substitute these values in the inequalities like this:

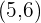




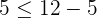

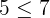

Hence, both the ordered pairs are true for the first inequality.
Now, we will check these ordered pairs for the second inequality  by substituting the values:
by substituting the values:

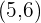




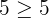
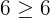
Hence, both the ordered pairs also satisfy the second inequality. It shows that the ordered pairs (4,5) and (5,6) are part of the solution set of the system of inequalities 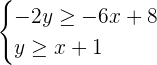 .
.
Check for the best Maths tutors on Superprof.
Check for an outstanding maths tutor near me here.













