Chapters

Exercise 1
Solve:
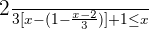
Exercise 2
Solve:
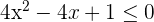
Exercise 3
Solve:
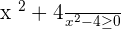
Exercise 4
Calculate the values of k for which the roots of the equation x² − 6x + k = 0 are two real and distinct numbers.
Exercise 5
Solve:
1 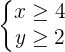
2 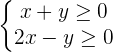
3 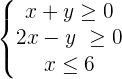
Exercise 6
Solve:

Exercise 7
Solve:
1 
2 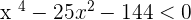
3 
Solution of exercise 1
Solve:
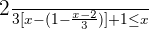

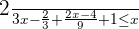
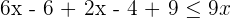



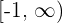
Solution of exercise 2
Solve:
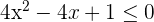

4x² − 4x + 1 ≤ 0
4x² − 4x + 1 = 0

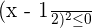
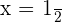
Solution of exercise 3
Solve:
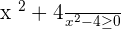
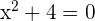
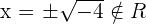
The numerator is always positive.
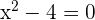
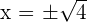
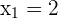
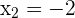
The denominator cannot be zero.

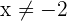
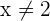
Therefore, the original inequality will be equivalent to:
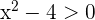

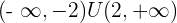
Get information about maths tuition in the UK.
Solution of exercise 4
Calculate the values of k for which the roots of the equation 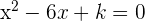 are two real and distinct numbers.
are two real and distinct numbers.
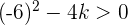
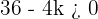

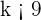

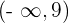
Solution of exercise 5
Solve:
1 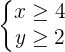



2 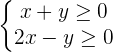
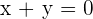
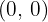
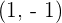
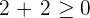
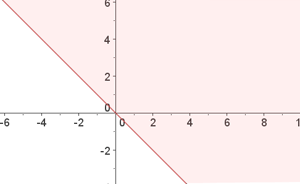
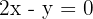
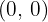

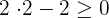


3 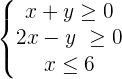
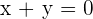
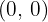

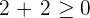

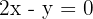
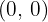

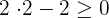


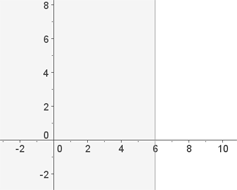
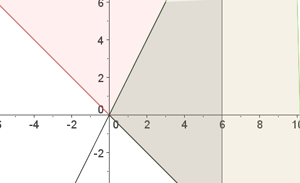
Solution of exercise 6
Solve:

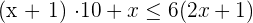

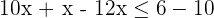

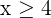
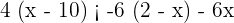



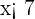

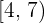
Solution of exercise 7
Solve:
1 

As the first factor is always positive, consider the sign of the 2nd factor.
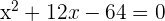
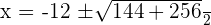

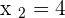
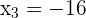

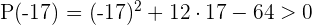
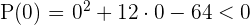
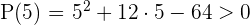

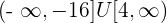
2 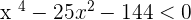
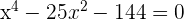
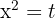
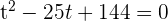



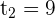
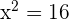
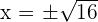

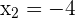
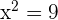
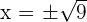
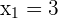


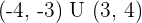
3 
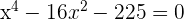
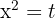


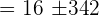
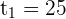
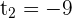

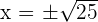

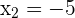
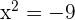

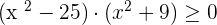
The second factor is always positive and nonzero, therefor, only consider the sign of the 1st factor.


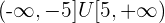
Learn more from Maths tutors near me on Superprof.
Check for outstanding maths tutors near me here.













