If a vehicle travels at a constant or uniform speed, the formula that relates distance, speed and time is:
Distance = speed 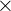 time
time
First Case Scenario
The vehicles are travelling towards one another.

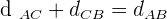
1 The time it takes for the cars to pass each other.
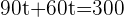


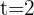 hours
hours
2 The time at which they passed each other.
They were at 11 of the morning.
3 The distance traveled by each at the time of them passing each other.
 miles
miles
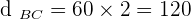 miles
miles
Second Case Scenario
The vehicles are travelling in the same direction from different starting points.

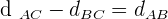
1. The time it takes for Car A to reach Car B:
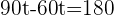
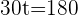
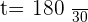
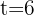 hours
hours
2. The time at which Car A reaches Car B:
Car A reaches Car B at 3 in the afternoon.
3. The distance traveled by each at the time of Car A reaching Car B:
 miles
miles
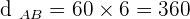 miles
miles
Check Superprof for different portfolios of maths tutors.
Third Case Scenario
The vehicles are travelling in the same direction with the same starting point.
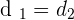
1. The time it takes for the second car to reach the first.

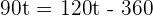

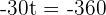
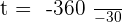
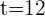 hours
hours
2. The distance from the city when the second car reaches the first.
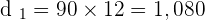 miles
miles
You can get a Maths tutor near me on Superprof.



3^x -2^y+2=10
2^x-3^x-2=2