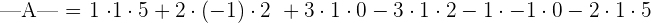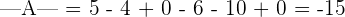Chapters

Introduction
We can calculate a special number from the square matrix known as determinant. A square matrix is a matrix that has equal number of rows and columns. It can be of any order, for instance a square matrix of order 2x2 means that there are two rows and two columns in it. Similarly, a square matrix of 3x3 means that its has three rows and three columns in it. We also have the square matrices of higher orders, for example 4x4, 5x5 and so on. We use vertical lines symbol || to denote the matrix.
If we are given a matrix B, then its determinant is denoted as |B|. The determinant of the matrix which has unequal number of rows and columns is not possible. The determinants of the matrices are useful in finding the inverse of a matrix, and solving system of linear equations. In this article, we will discuss how to find the determinant of the 3x3 matrix.
Determinant of a 3x3 Matrix
To find the determinant of a 3x3 matrix, we break down it into smaller components, for example the determinants of 2x2 matrices, so that it is easier to calculate. Consider the following 3x3 matrix:

The determinant of the matrix B will be calculated as:
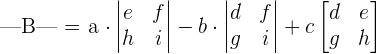
You can observe that :
- The elements in the first row; a, b and c are multiplied by the corresponding 2x2 matrix.
- The elements a is multiplied with a 2x2 matrix obtained after eliminating the row and column in which the element a is present.
- The same goes for other elements b and c.
Now, we will solve some of the examples in which we will compute the determinant of 3x3 matrix by hand.
Example 1
Calculate the determinant of the following matrix.
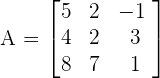
Solution
We will use the following formula to calculate the determinant of the above matrix:
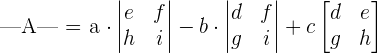
To decompose this matrix into smaller 2x2 matrices we need to look at the first row and multiply each element with the determinant of 2x2 matrix.
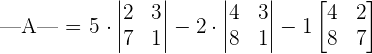
We know that the formula for finding the determinant of the following 2x2 matrix is:


We will employ this formula to calculate the determinants of the smaller 2x2 matrices.


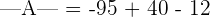
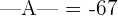
Hence, the determinant of the matrix A is -67.
Example 2
Calculate the determinant of the following matrix.
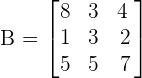
Solution
The following formula will be employed to calculate the determinant of 3x3 matrix.
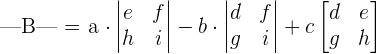
To break this matrix into smaller 2x2 matrices we need to look at the first row and multiply each element with the determinant of 2x2 matrix. The 2x2 matrix will be obtained after eliminating the row and column in which the element is present.
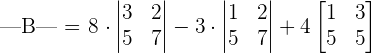
We know that the formula for finding the determinant of the following 2x2 matrix is:


We will employ this formula to calculate the determinants of the smaller 2x2 matrices.

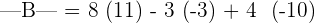
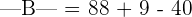

Hence, the determinant of the matrix B is 57.
Example 3
Calculate the determinant of the following matrix.
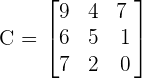
Solution
The following formula will be employed to calculate the determinant of above 3x3 matrix.

We will break this matrix into smaller 2x2 matrices, by looking at the first row and multiply each element with the determinant of 2x2 matrix. The 2x2 matrix will be obtained after eliminating the row and column in which the elements 9, 4 and 7 are present,
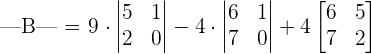
We know that the formula for finding the determinant of the following 2x2 matrix is:


We will employ this formula to calculate the determinants of the smaller 2x2 matrices.
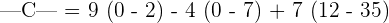

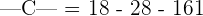
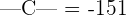
Hence, the determinant of the matrix C is -151.
Example 4
Calculate the determinant of the following matrix.
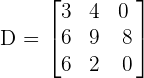
Solution
We will put the values from the above matrix in the following formula to compute the determinant.
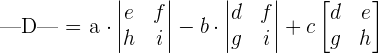
We will break this matrix into smaller 2x2 matrices, by looking at the first row and multiply each element with the determinant of 2x2 matrix. The 2x2 matrix will be obtained after eliminating the row and column in which the elements 3, 4 and 0 are present,
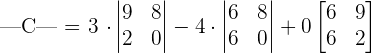
We know that the formula for finding the determinant of the following 2x2 matrix is:


We will employ this formula to calculate the determinants of the smaller 2x2 matrices.
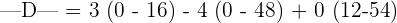


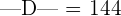
Hence, the determinant of the matrix D is 144.
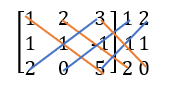
Rule of Sarrus
Sarrus' rule is also known as basketweave method. It is another method to calculate the determinant of a 3x3 matrix.

The terms with a − sign are formed by the elements of the secondary diagonal and those of the parallel diagonals with its corresponding opposite vertex.
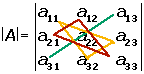
Example
Calculate the determinant of the following 3x3 matrix using Sarrus' rule.

Solution
Write the first two columns outside the determinant of the matrix and draw diagonal lines like this: