Elige la opción correcta:
1Sabiendo que  y que
y que  , calcula las restantes razones trigonométricas del ángulo
, calcula las restantes razones trigonométricas del ángulo 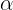 .
.
1En primer lugar, observemos que decir que 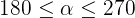 es lo mismo que decir que
es lo mismo que decir que 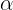 está en el tercer cuadrante. Entonces, su coseno es negativo y su tangente es positiva.
está en el tercer cuadrante. Entonces, su coseno es negativo y su tangente es positiva.
2Para encontrar el coseno, sustituimos el valor de 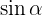 en la identidad trigonométrica
en la identidad trigonométrica 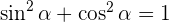

Despejando  y sabiendo que coseno es negativo en el tercer cuadrante se obtiene
y sabiendo que coseno es negativo en el tercer cuadrante se obtiene

3Para encontrar la tangente, sustituimos el valor de 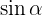 y
y  en la identidad trigonométrica
en la identidad trigonométrica 
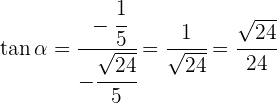
2Sabiendo que  y que
y que  , calcula las restantes razones trigonométricas del ángulo
, calcula las restantes razones trigonométricas del ángulo 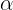 .
.
Si prefieres aprender desde casa, ¿por qué no buscas un profesor de matematicas online? ¡La primera clase es gratis!
1En primer lugar, observemos que decir que  es lo mismo que decir que
es lo mismo que decir que  está en el primer cuadrante. Entonces, su seno y su tangente son positivos.
está en el primer cuadrante. Entonces, su seno y su tangente son positivos.
2Para encontrar el seno, sustituimos el valor de  en la identidad trigonométrica
en la identidad trigonométrica 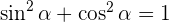
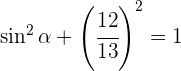
Despejando  y sabiendo que seno es positivo en el primer cuadrante se obtiene
y sabiendo que seno es positivo en el primer cuadrante se obtiene

3Para encontrar la tangente, sustituimos el valor de 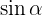 y
y  en la identidad trigonométrica
en la identidad trigonométrica 

3Sabiendo que 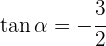 y que
y que 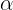 está en el segundo cuadrante, calcula las restantes razones trigonométricas del ángulo
está en el segundo cuadrante, calcula las restantes razones trigonométricas del ángulo 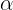 .
.
1Como 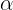 está en el segundo cuadrante, su seno es positivo y su coseno es negativo.
está en el segundo cuadrante, su seno es positivo y su coseno es negativo.
2Para encontrar el coseno, sustituimos el valor de 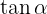 en la identidad trigonométrica
en la identidad trigonométrica 
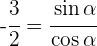
Expresamos  en término de
en término de 
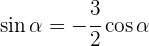
Para encontrar el coseno, sustituimos el valor de 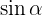 en la identidad trigonométrica
en la identidad trigonométrica 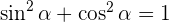

Despejando  y sabiendo que es negativo en el segundo cuadrante se obtiene
y sabiendo que es negativo en el segundo cuadrante se obtiene
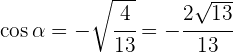
3Para encontrar el seno, sustituimos el valor de  en
en 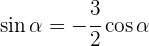
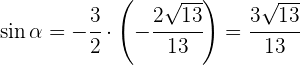
4Sabiendo que 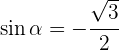 y que
y que 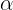 está en el cuarto cuadrante, calcula las restantes razones trigonométricas del ángulo
está en el cuarto cuadrante, calcula las restantes razones trigonométricas del ángulo 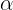 .
.
1Como 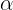 está en el cuarto cuadrante, su seno es negativo y su coseno es positivo.
está en el cuarto cuadrante, su seno es negativo y su coseno es positivo.
2Para encontrar el coseno, sustituimos el valor de 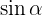 en la identidad trigonométrica
en la identidad trigonométrica 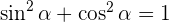

Despejando  y sabiendo que coseno es positivo en el cuarto cuadrante se obtiene
y sabiendo que coseno es positivo en el cuarto cuadrante se obtiene
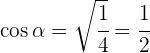
3Para encontrar la tangente, sustituimos el valor de 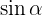 y
y  en la identidad trigonométrica
en la identidad trigonométrica 

5Sabiendo que  y que
y que  , calcula las restantes razones trigonométricas del ángulo
, calcula las restantes razones trigonométricas del ángulo 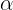 .
.
1En primer lugar, observemos que decir que  es lo mismo que decir que
es lo mismo que decir que 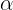 está en el cuarto cuadrante. Entonces, su seno es negativo y su coseno es positivo.
está en el cuarto cuadrante. Entonces, su seno es negativo y su coseno es positivo.
2Para encontrar el coseno, sustituimos el valor de 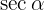 en la identidad trigonométrica
en la identidad trigonométrica 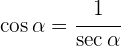
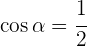
3Para encontrar el seno, sustituimos el valor de  en la identidad trigonométrica
en la identidad trigonométrica 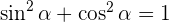
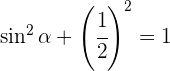
Despejando  y sabiendo que seno es negativo en el cuarto cuadrante se obtiene
y sabiendo que seno es negativo en el cuarto cuadrante se obtiene
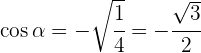
6Sabiendo que  y que
y que 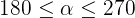 , calcula las restantes razones trigonométricas, del ángulo
, calcula las restantes razones trigonométricas, del ángulo 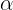 .
.
En primer lugar, observemos que decir que 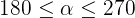 es lo mismo que decir que
es lo mismo que decir que 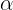 está en el tercer cuadrante. Entonces, su seno es negativo, su coseno negativo y su tangente es positiva.
está en el tercer cuadrante. Entonces, su seno es negativo, su coseno negativo y su tangente es positiva.
2Para encontrar el coseno, sustituimos el valor de 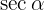 en la identidad trigonométrica
en la identidad trigonométrica 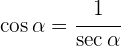
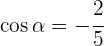
3Para encontrar el seno, sustituimos el valor de  en la identidad trigonométrica
en la identidad trigonométrica 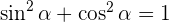
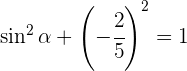
Despejando  y sabiendo que seno es negativo en el tercer cuadrante se obtiene
y sabiendo que seno es negativo en el tercer cuadrante se obtiene
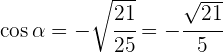
7Sabiendo que 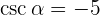 y que
y que 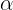 está en el cuarto cuadrante, calcula las restantes razones trigonométricas del ángulo
está en el cuarto cuadrante, calcula las restantes razones trigonométricas del ángulo 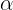 .
.
1En primer lugar, observemos que como 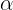 está en el cuarto cuadrante, su seno es negativo, su coseno positivo y su tangente negativa.
está en el cuarto cuadrante, su seno es negativo, su coseno positivo y su tangente negativa.
2Para encontrar el seno, sustituimos el valor de  en la identidad trigonométrica
en la identidad trigonométrica 

3Para encontrar el coseno, sustituimos el valor de 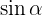 en la identidad trigonométrica
en la identidad trigonométrica 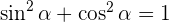

Despejando  y sabiendo que coseno es positivo en el cuarto cuadrante se obtiene
y sabiendo que coseno es positivo en el cuarto cuadrante se obtiene
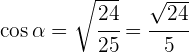
8Sabiendo que 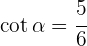 , calcula las restantes razones trigonométricas del ángulo
, calcula las restantes razones trigonométricas del ángulo 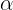 .
.
1Como  es positivo, entonces se encuentra en el primer o tercer cuadrante, y su seno y coseno son positivos o negativos.
es positivo, entonces se encuentra en el primer o tercer cuadrante, y su seno y coseno son positivos o negativos.
2Para encontrar el seno, sustituimos el valor de 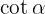 en la identidad trigonométrica
en la identidad trigonométrica 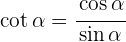

Expresamos  en término de
en término de 

Para encontrar el seno, sustituimos el valor de  en la identidad trigonométrica
en la identidad trigonométrica 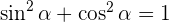

Despejando  y sabiendo que es positivo en el primer cuadrante y negativo en el tercero, se obtiene
y sabiendo que es positivo en el primer cuadrante y negativo en el tercero, se obtiene
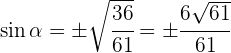
3Para encontrar el coseno, sustituimos el valor de 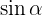 en
en 
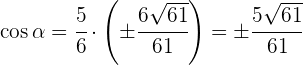
9Sabiendo que  , calcula las restantes razones trigonométricas del ángulo
, calcula las restantes razones trigonométricas del ángulo 
1En primer lugar, observemos  es negativo en el tercer y cuarto cuadrante. Entonces, su coseno es negativo y su tangente es positiva en el tercer cuadrante; mientras que su coseno es positivo y su tangente negativo en el cuarto cuadrante.
es negativo en el tercer y cuarto cuadrante. Entonces, su coseno es negativo y su tangente es positiva en el tercer cuadrante; mientras que su coseno es positivo y su tangente negativo en el cuarto cuadrante.
2Para encontrar el coseno, sustituimos el valor de 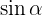 en la identidad trigonométrica
en la identidad trigonométrica 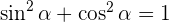

Despejando  se obtiene
se obtiene
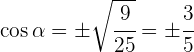
3Para encontrar la tangente, sustituimos el valor de 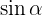 y
y  en la identidad trigonométrica
en la identidad trigonométrica 

10Sabiendo que  , calcula las restantes razones trigonométricas del ángulo
, calcula las restantes razones trigonométricas del ángulo  .
.
1Como 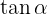 es positivo, entonces se encuentra en el primer o tercer cuadrante, y su seno y coseno son positivos o negativos.
es positivo, entonces se encuentra en el primer o tercer cuadrante, y su seno y coseno son positivos o negativos.
2Para encontrar el coseno, sustituimos el valor de 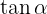 en la identidad trigonométrica
en la identidad trigonométrica 

Expresamos  en término de
en término de 
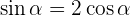
Para encontrar el coseno, sustituimos el valor de 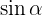 en la identidad trigonométrica
en la identidad trigonométrica 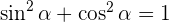
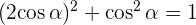
Despejando  y sabiendo que es positivo en el primer cuadrante y negativo en el tercero, se obtiene
y sabiendo que es positivo en el primer cuadrante y negativo en el tercero, se obtiene

3Para encontrar el seno, sustituimos el valor de  en
en 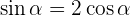

Si tienes dudas puedes consultar la teoría



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
C=49 A=54 a=72
b = 40,2 a = 31, 5 B = 112 °20
Encontrar la solucion principal de la ecuación trigonometría asenX+bcosX = cl donde a, b y c son numeros reales y a≠0, b≠0
Ayúdeme en éste ejercicio por favor.
Complete el siguiente triángulo rectangulo, calculando sus ángulos en cada unos de los vértices:
* Ángulo del vértice (A) es alpha, y su dimensión es 7
* Hipotenusa es b.
* Ángulo del vértice (C) es beta, y su dimensión es raíz de 5.
Demostrar que los ángulos del triángulo es 90°, aplicando cada uno de los procesos.
Muy amable, gracias 🫂
Sj dos lados de un triangulo miden 200m y 18cm y el angulo comprendido, entre ello Calcular el área def trianguts
Lucy ayúdeme en este trabajo
Seno=30÷c
Resolver los siguientes Triángulos Oblicuángulos, aplicando las Leyes
del Seno, Coseno y/o Tangente:
o a = 41; b = 19,5; c= 32,48
o a=5,312; b = 10,913; c = 13
o a = 32,45; b = 27,21; C = 66° 56′
b = 50; c = 66,6; A = 83° 26′
o a=41; B = 27°50′; C = 51°
O
a= 78,6; A = 83°26′; B = 39°13′
me pueden ayudar es urgente