Temas
- Conversión de grados
- Cálculo de razones trigonométricas a partir de una dada
- Cálculo de razones trigonométricas a partir del ángulo
- Resolución de triángulos
- Problemas de la vida cotidiana
- Problema de distancia entre dos ciudades
- Problema de altura de una cometa
- Problema de la altura de un edificio
- Demostración de identidades trigonométricas
A continuación encontrarás una serie de problemas y ejercicios que se resuelven empleando trigonometría. En las soluciones te describimos a detalle cada uno de los pasos realizados

Conversión de grados
1 Convierte los siguientes ángulos de radianes a sexagesimal
a 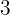
b 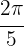
c 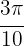
Recordemos que la fórmula para calcular un ángulo en radianes a grados es

donde  es el ángulo en radianes. Por lo tanto, los ángulos en grados son:
es el ángulo en radianes. Por lo tanto, los ángulos en grados son:
a 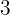
Aquí tenemos que 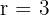 . Por lo tanto, los grados son
. Por lo tanto, los grados son
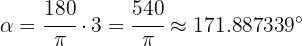
Para obtener los minutos, multiplicamos la parte decimal por 60:
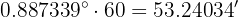
Para obtener los segundos, multiplicamos de nuevo la parte decimal por 60:
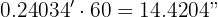
Por lo tanto, el ángulo en sexagesimal es 
b 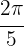
Al igual que en el ejercicio anterior, utilizamos la fórmula

c 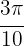
Aquí también utilizamos la misma fórmula:

2 Expresa en radianes los siguientes ángulos:
a 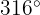
b 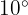
c 
La fórmula para convertir de grados a radianes es muy simpliar a la anterior
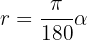
Así, los ángulos son:
a 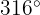
Utilizamos la fórmula
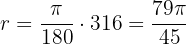
Por lo tanto, el ángulo mide 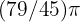 radianes.
radianes.
b 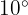
Utilizamos la fórmula
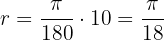
Por lo tanto, el ángulo mide 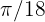 radianes.
radianes.
c 
Utilizamos la fórmula

Que no se puede simplificar ya que 127 es primo. Por lo tanto, el ángulo mide 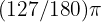 .
.
Cálculo de razones trigonométricas a partir de una dada
3 Sabiendo que 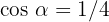 y que
y que 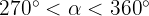 , calcula las razones trigonométricas restantes para el ángulo
, calcula las razones trigonométricas restantes para el ángulo  .
.
En primer lugar, sabemos que el ángulo se encuentra en el cuarto cuadrante del plano cartesiano. En este cuadrante tenemos que  pero
pero  . Por tanto,
. Por tanto,
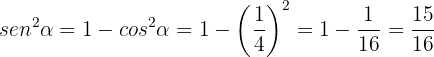
De aquí se sigue que
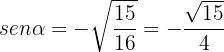
Como ya tenemos  y
y  , entonces las otras identidades son más sencillas.
, entonces las otras identidades son más sencillas.

Observemos que tanto en la cotangente como en la cosecante se puede racionalizar el resultado. Por lo que también es correcto si tuviéramos

Lo cual se obtiene si multiplicamos los resultados anteriores por  , con lo que evitaríamos tener radicales en el denominador.
, con lo que evitaríamos tener radicales en el denominador.
4 Sabiendo que 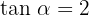 y que
y que 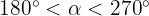 , calcula las restantes razones trigonométricas para el ángulo
, calcula las restantes razones trigonométricas para el ángulo  .
.
El ángulo  se encuentra en el 3er cuadrante del plano cartesiano. De aquí sabemos que
se encuentra en el 3er cuadrante del plano cartesiano. De aquí sabemos que  y
y  .
.
Por otro lado, la tangente se relaciona con la secante con su identidad pitagórica:
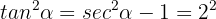
De donde tenemos que

Como  , entonces
, entonces  . Por lo tanto,
. Por lo tanto,
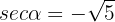
De aquí se sigue que

Notemos que 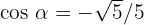 también es una respuesta correcta (al racionalizar el resultado anterior).
también es una respuesta correcta (al racionalizar el resultado anterior).
Sabemos, también, que  . De aquí se sigue que
. De aquí se sigue que

Las dos identidades que faltan se calculan de forma muy sencilla:

y

5 Sabieno que 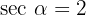 y que
y que 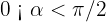 , calcula las razones trigonométricas restantes para el ángulo
, calcula las razones trigonométricas restantes para el ángulo  .
.
Notemos, en primer lugar, que el ángulo está en radianes. Además, nos encontramos en el primer cuadrante del plano cartesiano, por lo que 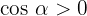 y
y  .
.
Por otro lado, la secante se relaciona con  por medio de su identidad pitagórica:
por medio de su identidad pitagórica:
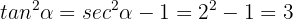
Además, 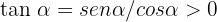 ya que
ya que  y
y  , por lo que
, por lo que
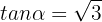
Asimismo,
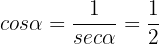
Y como tenemos que  , entonces se sigue que
, entonces se sigue que
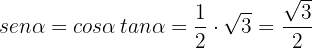
Con esto las últimas dos identidades trigonométricas son muy sencillas de calcular:
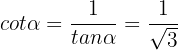
y

Cálculo de razones trigonométricas a partir del ángulo
6 Calcula el seno, coseno y tangente para los siguientes ángulos:
a 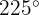
b 
Aquí asumiremos ya tenemos memorizadas el seno y el coseno para algunos ángulos muy comunes (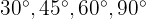 , etcétera):
, etcétera):
a 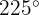
Para calcular el seno del ángulo, utilizaremos algunas identidades de traslación. Observemos que
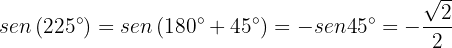
Similarmente,

Por último

b 
Al igual que en el caso anterior, utilizaremos algunas identidades de traslación. Observemos que

Similarmente,

Por último

7 Calcula las razones trigonométricas para los siguientes ángulos:
a 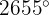
b 
a 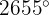
Primero debemos encontrar un ángulo que esté entre  y
y 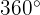 y que igual a
y que igual a 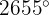 . Para esto, dividimos 2655 entre 360 y el residuo será el ángulo que buscamos:
. Para esto, dividimos 2655 entre 360 y el residuo será el ángulo que buscamos:

donde el residuo es 135. Por lo tanto

Similarmente,

Por último,
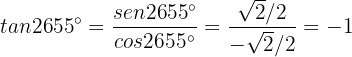
b 
Este es muy similar al caso anterior. Dividimos primero 840 entre 360 y nos quedamos con el residuo:
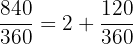
Por lo que 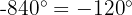 . De este modo:
. De este modo:

Similarmente,

Por último,

Resolución de triángulos
8 Dado el triángulo rectángulo ABC, rectángulo en el ángulo  , se conoce que
, se conoce que  y
y 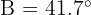 . Encuentra los otros ángulos y lados.
. Encuentra los otros ángulos y lados.
Observemos el siguiente triángulo:
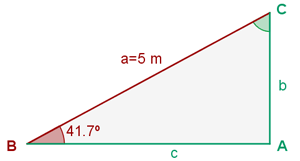
Ahí podemos ver los datos que nos faltan (los lados  ,
,  y el ángulo
y el ángulo  ). El más sencillo es el ángulo
). El más sencillo es el ángulo  , puesto que
, puesto que  . Por lo que
. Por lo que
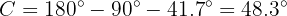
Como el triángulo es rectángulo, entonces podemos utilizar funciones trigonométricas para calcular la longitud de los lados restantes. Sabemos que

por lo que
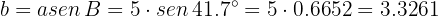
Similarmente, como  , entonces
, entonces

Con lo que ya encontramos todos los datos faltantes.
9 Del triángulo ABC, rectángulo en el ángulo  , conocemos que
, conocemos que 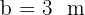 y
y 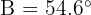 . Encuentra los otros ángulos y lados.
. Encuentra los otros ángulos y lados.
Observemos el triángulo de este ejercicio:
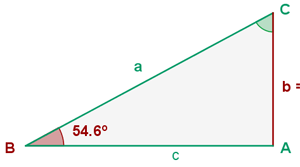
Ahí podemos ver los datos que nos faltan (los lados  ,
,  y el ángulo
y el ángulo  ). Al igual que en el caso anterior, el más sencillo es el ángulo
). Al igual que en el caso anterior, el más sencillo es el ángulo  , ya que
, ya que  . Por lo que
. Por lo que
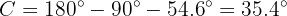
Ahora no tenemos la hipotenusa. Por tanto debemos utilizar la tangente para empezar:
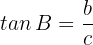
por lo que
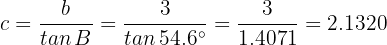
Similarmente, como  , entonces
, entonces
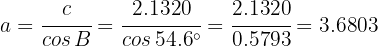
Con lo que ya encontramos todos los datos faltantes.
10 Del triángulo ABC, rectángulo en el ángulo  , conocemos que
, conocemos que  y
y 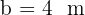 . Encuentra los ángulos agudos y el lado restante.
. Encuentra los ángulos agudos y el lado restante.
Observemos el triángulo:
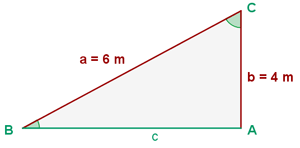
Los datos que nos faltan son el cateto  y los ángulos
y los ángulos  y
y  . Por el teorema de pitágoras, sabemos que
. Por el teorema de pitágoras, sabemos que  , de modo que
, de modo que
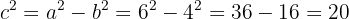
Así, 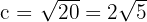 . Además,
. Además,
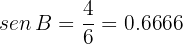
Por lo que 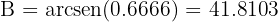 . Por último, debido a que los ángulos suman
. Por último, debido a que los ángulos suman  :
:
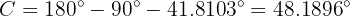
Con lo que terminamos de resolver el triángulo.
11 Dado un triángulo  , se conoce que
, se conoce que 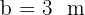 ,
,  y
y 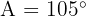 . Encuentra los ángulos y el lado restantes.
. Encuentra los ángulos y el lado restantes.
Observemos que este triángulo no es rectángulo. De hecho, el triángulo se muestra en la siguiente figura:

Donde vemos que nos faltan los ángulos  ,
,  y el lado
y el lado  . Como el triángulo no es rectángulo, entonces no podemos utilizar el teorema de pitágoras, pero sí podemos utilizar el teorema de los cosenos:
. Como el triángulo no es rectángulo, entonces no podemos utilizar el teorema de pitágoras, pero sí podemos utilizar el teorema de los cosenos:

donde ya tenemos todos los datos. Tenemos

Por lo tanto  . Con esto, ya podemos calcular cualquiera de los ángulos restantes utilizando la ley de los senos:
. Con esto, ya podemos calcular cualquiera de los ángulos restantes utilizando la ley de los senos:

de donde se sigue que

de donde se sigue que 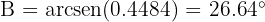 .
.
Por último,
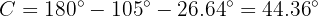
con lo que resolvemos todo el triángulo por completo.
Problemas de la vida cotidiana
12 Un árbol de 50 metros de altura proyecta una sombra de 60 metros de longitud. Encuentra el ángulo de elvación del Sol en ese momento.
Observemos que el árbol (lado  ) y la sombra (lado
) y la sombra (lado  ) forman el siguiente triángulo:
) forman el siguiente triángulo:

Notemos que no es necesario calcular el lado  . Buscamos el ángulo
. Buscamos el ángulo  , cuya tangente está dada por
, cuya tangente está dada por
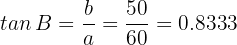
Utilizando el arcotangente, obtenemos
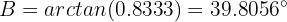
Que es el ángulo que buscábamos.
13 Un dirigible está volando a 800 metros de altura. Observa un pueblo con un ángulo de depresión de 12°. ¿Qué distancia debe recorrer el dirigible en linea recta, manteniendo la altura, para estar exactamente sobre el pueblo?
Observemos que entre el pueblo y el dirigible se forma el siguiente triángulo:

donde la distancia incógnita la denotamos por  . La altura del dirigible la denotamos por
. La altura del dirigible la denotamos por  y el ángulo de depresión coincide con el ángulo
y el ángulo de depresión coincide con el ángulo 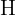 .
.
Sabemos que la tangente de 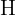 se calcula utilizando
se calcula utilizando

por lo que
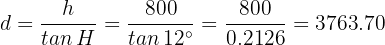
Por tanto, el dirigible debe recorrer 3763.70 metros, o 3.764 km.
14 Hallar el radio de una circunferencia donde una cuerda de 24.6 metros tiene un arco de 70° correspondiente.
Observemos la siguiente figura:
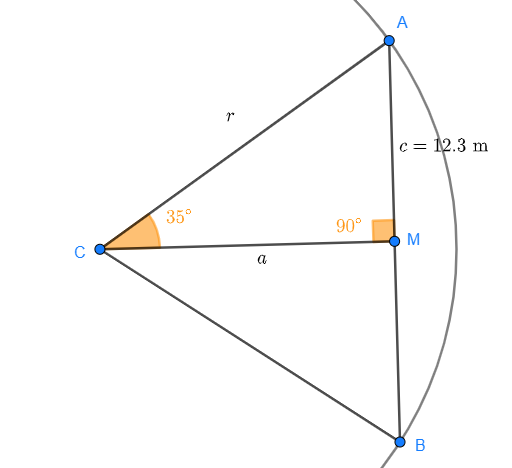
Notemos que se forma un triángulo rectángulo con los puntos  donde
donde  es el punto medio del arco.
es el punto medio del arco.
El radio  es la hipotenusa de este triángulo, la longitud de
es la hipotenusa de este triángulo, la longitud de  es la mitad de la cuerda, es decir,
es la mitad de la cuerda, es decir,
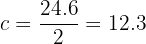
y el ángulo  mide
mide  (la mitad del arco). Sabemos que
(la mitad del arco). Sabemos que

ya que  es la hipotenusa. Por tanto,
es la hipotenusa. Por tanto,

por lo tanto, el radio mide 21.44 metros.
15 Calcular el área de una parcela triángulo, sabiendo que dos de sus lados miden 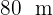 y
y 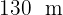 , y el ángulo entre ellos es de 70°
, y el ángulo entre ellos es de 70°
Existen varias formas de resolver este problema. Podemos utilizar la fórmula de Herón o podemos intentar calcular alguna de sus alturas. Primero observemos el triángulo:

Donde 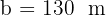 ,
, 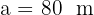 y
y 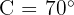 .
.
Si trazamos la altura que es perpendicular a  , notemos que se forma un triángulo rectángulo donde
, notemos que se forma un triángulo rectángulo donde  es un cateto y
es un cateto y  es la hipotenusa. Además, notemos que el seno de
es la hipotenusa. Además, notemos que el seno de  es
es
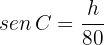
de modo que
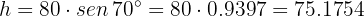
Por lo tanto, el área es
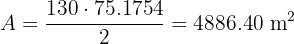
16 Calcula la altura de un árbol, sabiendo que desde un punto del terreno se observa su copa en un ángulo de 30° sobre el nivel de la tierra, y si nos acercamos 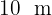 entonces la copa se observa en un ángulo de 60° sobre la tierra.
entonces la copa se observa en un ángulo de 60° sobre la tierra.
Observemos la siguiente figura, la cual es una representación del problema:
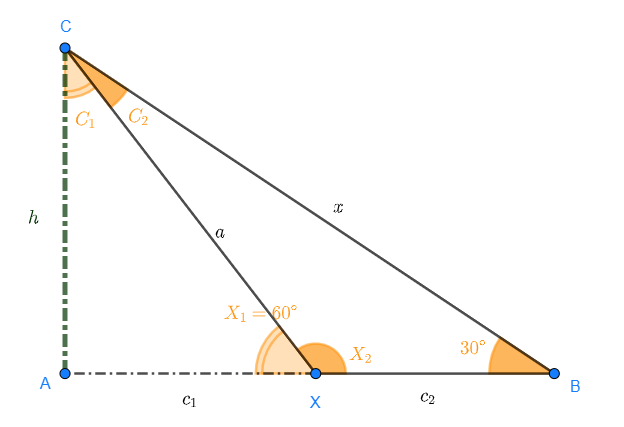
Notemos que hay varias formas de resolver este problema. Una es encontrar la distancia 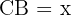 resolviendo el triángulo
resolviendo el triángulo  ; después utilizamos esa distancia para encontrar la altura.
; después utilizamos esa distancia para encontrar la altura.
Para resolver el triángulo, notemos que el ángulo 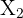 del triángulo
del triángulo  es
es
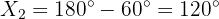
por tanto, ya podemos utilizar el teorema de los senos para resolver triángulo. Sin embargo, necesitamos primero al ángulo 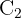 , que es,
, que es,

Por el teorema de los senos se tiene que
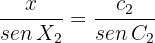
donde
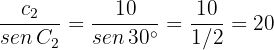
Por lo tanto,
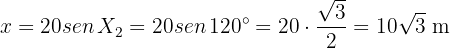
Con esto ya podemos calcular la altura del árbol. Notemos que el triángulo  es rectángulo. Por tanto,
es rectángulo. Por tanto,
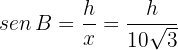
Por tanto,

Por tanto, el árbol mide 8.66 metros de altura.
17 Un octágono regular tiene lados que miden 12 metros. Encuentra los radios de la circunferencia inscrita y circunscrita.
Observa la siguiente figura de un octágono con sus circunferencias inscritas y circunscritas:
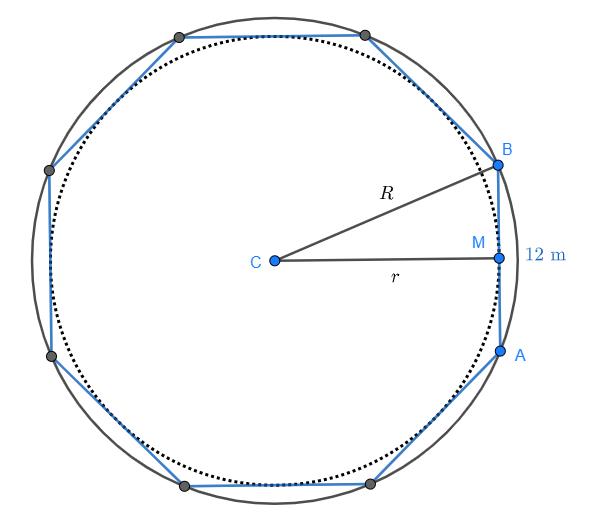
Notemos que se forma un triángulo rectángulo entre los puntos  donde
donde  es el punto medio de cualquier lado del octágono. Observemos con más detalle este triángulo rectángulo:
es el punto medio de cualquier lado del octágono. Observemos con más detalle este triángulo rectángulo:
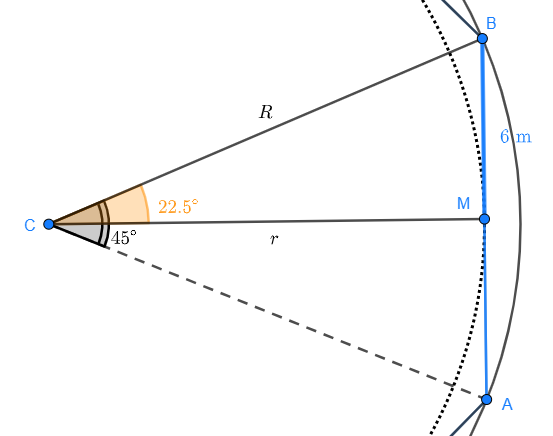
Sabemos que el ángulo  . Por lo que el ángulo
. Por lo que el ángulo  del triángulo rectángulo será
del triángulo rectángulo será 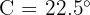 . Además, el lado
. Además, el lado 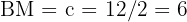 .
.
Los dos lados del triángulo que nos faltan son, de hecho, los radios de las circunferencias. Empezando por el lado  , tenemos que
, tenemos que

Por lo que
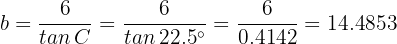
Por lo tanto, el radio  de la circunferencia inscrita es 14.49 metros.
de la circunferencia inscrita es 14.49 metros.
Luego, el lado  satisface
satisface

de modo que 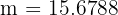 . Es decir, el radio
. Es decir, el radio  de la circunferencia circunscrita es 15.68 metros.
de la circunferencia circunscrita es 15.68 metros.
Problema de distancia entre dos ciudades
18 Tres ciudades 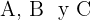 se encuentran distribuidas de forma triangular y sus caminos son en línea recta. Si la distancia de
se encuentran distribuidas de forma triangular y sus caminos son en línea recta. Si la distancia de  a
a  es de 12 km, la distancia de
es de 12 km, la distancia de  a
a  es de 10 km y el ángulo
es de 10 km y el ángulo 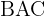 es
es 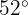 . Encuentra la distancia entre las ciudades
. Encuentra la distancia entre las ciudades  .
.
La figura que representa el problema forma un triángulo

Notemos que para calcular el lado  basta aplicar la ley de los cosenos
basta aplicar la ley de los cosenos

Realizando las operaciones, obtenemos
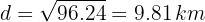
Que es la distancia entre las ciudades  que buscábamos.
que buscábamos.
Problema de altura de una cometa
19 Pedro vuela una cometa para lo cual emplea 40 m de cuerda. Si el ángulo de elevación es de 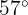 , ¿cuál es la altura de la cometa respecto al piso?
, ¿cuál es la altura de la cometa respecto al piso?
Observemos que la cuerda de cometa (lado  ) y la proyección de la cometa al piso (lado
) y la proyección de la cometa al piso (lado  ) forman el siguiente triángulo rectángulo:
) forman el siguiente triángulo rectángulo:
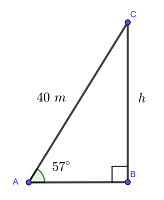
Notemos que la expresión del seno del ángulo  es:
es:
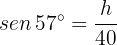
Despejando la altura  , obtenemos
, obtenemos
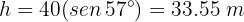
Que es la altura que buscábamos.
Problema de la altura de un edificio
20 Un edificio proyecta una sombra de 60 metros de longitud, siendo 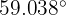 el ángulo de elevación del sol en ese momento. Encuentra la altura del edificio.
el ángulo de elevación del sol en ese momento. Encuentra la altura del edificio.
Observemos que el edificio (lado  ) y la sombra (lado
) y la sombra (lado 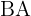 ) forman el siguiente triángulo rectángulo:
) forman el siguiente triángulo rectángulo:
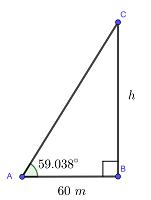
Notemos que la expresión de la tangente del ángulo de 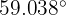 , está dada por
, está dada por
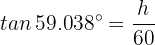
Despejando la altura  , obtenemos
, obtenemos

Que es la altura que buscábamos.
Demostración de identidades trigonométricas
21 Demuestra las siguientes identidades trigonométricas:
a 
b 
c 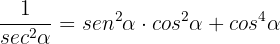
a 
Empezamos escribiendo a 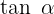 y
y 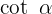 con su definición en senos y cosenos:
con su definición en senos y cosenos:

Después realizamos la suma de las fracciones (con el común denominador):

Notamos que 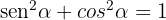 , por lo que
, por lo que
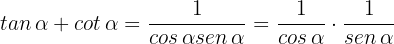
las cuales son las definiciones de  y
y  . Por tanto,
. Por tanto,
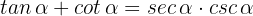
b 
Aquí conviene empezar del lado derecho de la ecuación:

Factorizamos el 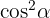
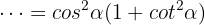
Recordemos que la identidad pitagórica de la 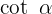 es
es 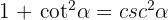 , de modo que tenemos
, de modo que tenemos
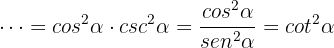
que era justo lo que queriamos demostrar.
c 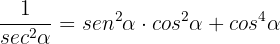
Aquí tambien conviene empezar del lado derecho de la identidad, factorizando 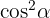 :
:
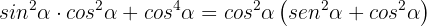
Notamos que 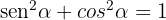 , por lo que
, por lo que
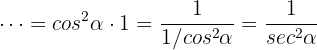
que era lo que buscábamos demostrar.
22 Demuestra las siguientes identidades trigonométricas:
a 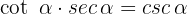
b 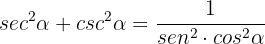
a 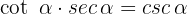
La forma más sencilla de demostrar esta identidad es empezar del lado izquiero y escribir las relaciones en términos de senos y cosenos:

Ya que  se cancela. Esta identidad era posible demostrarla en una sola línea.
se cancela. Esta identidad era posible demostrarla en una sola línea.
b 
Empezamos del lado izquierdo y escribimos las relaciones en términos de senos y cosenos:
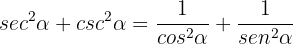
Luego sumamos las fracciones utilizando el común denominador:
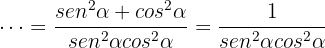
ya que 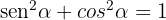 . Por lo tanto, llegamos a lo que queríamos demostrar.
. Por lo tanto, llegamos a lo que queríamos demostrar.
¿Y si buscas un profe de mates en Superprof?













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
C=49 A=54 a=72
b = 40,2 a = 31, 5 B = 112 °20
Encontrar la solucion principal de la ecuación trigonometría asenX+bcosX = cl donde a, b y c son numeros reales y a≠0, b≠0
Ayúdeme en éste ejercicio por favor.
Complete el siguiente triángulo rectangulo, calculando sus ángulos en cada unos de los vértices:
* Ángulo del vértice (A) es alpha, y su dimensión es 7
* Hipotenusa es b.
* Ángulo del vértice (C) es beta, y su dimensión es raíz de 5.
Demostrar que los ángulos del triángulo es 90°, aplicando cada uno de los procesos.
Muy amable, gracias 🫂
Sj dos lados de un triangulo miden 200m y 18cm y el angulo comprendido, entre ello Calcular el área def trianguts
Lucy ayúdeme en este trabajo
Seno=30÷c
Resolver los siguientes Triángulos Oblicuángulos, aplicando las Leyes
del Seno, Coseno y/o Tangente:
o a = 41; b = 19,5; c= 32,48
o a=5,312; b = 10,913; c = 13
o a = 32,45; b = 27,21; C = 66° 56′
b = 50; c = 66,6; A = 83° 26′
o a=41; B = 27°50′; C = 51°
O
a= 78,6; A = 83°26′; B = 39°13′
me pueden ayudar es urgente