Temas

La razón que existe entre un lado de un triángulo oblicuángulo y el seno del ángulo opuesto a dicho lado es proporcional a la misma razón entre los lados y ángulos restantes, es decir:
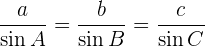
Esta relación es conocida como la ley de senos.
III Resolver un triángulo conociendo dos lados y un ángulo opuesto
Supongamos que tenemos  y
y  , es decir,
, es decir,

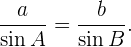 Se tiene los siguientes casos:
Se tiene los siguientes casos:
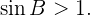 No hay solución
No hay solución 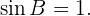 Triángulo rectángulo
Triángulo rectángulo
 Una o dos soluciones
Una o dos soluciones
Ejemplos de los casos
1 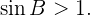 No hay solución
No hay solución
 ,
, 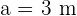 y
y 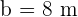 . Por la ley de senos se tiene la siguiente relación:
. Por la ley de senos se tiene la siguiente relación: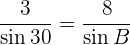
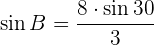
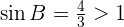
Como el seno de un ángulo nunca puede ser mayor que 1, el problema no tiene solución.
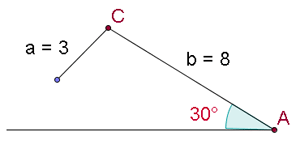
La figura muestra la imposibilidad de que exista el triángulo planteado.
2 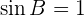 Triángulo rectángulo
Triángulo rectángulo
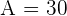 ,
, 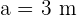 y
y 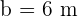 .Por la ley de senos se tiene la siguiente relación:
.Por la ley de senos se tiene la siguiente relación: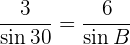
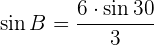

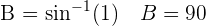 Por lo tanto tenemos un triángulo rectángulo, como se muestra en la siguiente imagen.
Por lo tanto tenemos un triángulo rectángulo, como se muestra en la siguiente imagen. 
Ahora calculamos el ángulo restante y el valor de los lados faltantes.
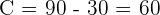
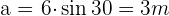

3 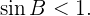 Una o dos soluciones
Una o dos soluciones
1 Resuelve el triángulo de datos: 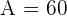 ,
,  y
y 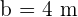 . Por la ley de senos se tiene la siguiente relación:
. Por la ley de senos se tiene la siguiente relación: 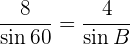
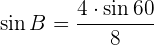
 Entonces tenemos dos opciones:
Entonces tenemos dos opciones: Como
Como  solo es válida la solución:
solo es válida la solución: 
Calculamos el lado faltante,
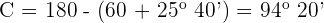
Aplicando de nuevo la ley de senos:

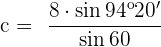
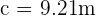
2 Resuelve el triángulo de datos: 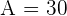 ,
, 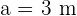 y
y 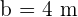 .
.
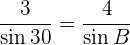
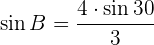

Entonces,
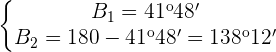
Como  solo son válidas las dos soluciones
solo son válidas las dos soluciones
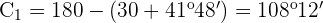
Aplicando de nuevo la ley de senos:
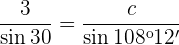
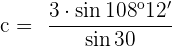
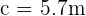
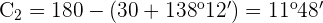
Aplicando de nuevo la ley de senos:
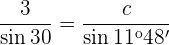
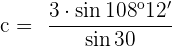
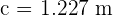














Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
C=49 A=54 a=72
b = 40,2 a = 31, 5 B = 112 °20
Encontrar la solucion principal de la ecuación trigonometría asenX+bcosX = cl donde a, b y c son numeros reales y a≠0, b≠0
Ayúdeme en éste ejercicio por favor.
Complete el siguiente triángulo rectangulo, calculando sus ángulos en cada unos de los vértices:
* Ángulo del vértice (A) es alpha, y su dimensión es 7
* Hipotenusa es b.
* Ángulo del vértice (C) es beta, y su dimensión es raíz de 5.
Demostrar que los ángulos del triángulo es 90°, aplicando cada uno de los procesos.
Muy amable, gracias 🫂
Sj dos lados de un triangulo miden 200m y 18cm y el angulo comprendido, entre ello Calcular el área def trianguts
Lucy ayúdeme en este trabajo
Seno=30÷c
Resolver los siguientes Triángulos Oblicuángulos, aplicando las Leyes
del Seno, Coseno y/o Tangente:
o a = 41; b = 19,5; c= 32,48
o a=5,312; b = 10,913; c = 13
o a = 32,45; b = 27,21; C = 66° 56′
b = 50; c = 66,6; A = 83° 26′
o a=41; B = 27°50′; C = 51°
O
a= 78,6; A = 83°26′; B = 39°13′
me pueden ayudar es urgente