1 Encontrar el término general de las siguientes sucesiones:
a 
b 
c 
a Encontrar el término general de la sucesión:
- La diferencia entre los numeradores consecutivos es
 , por lo cual podemos expresar los numeradores como
, por lo cual podemos expresar los numeradores como  .
. - El denominador es una progresión aritmética, con
 , por lo cual podemos expresar los numeradores como
, por lo cual podemos expresar los numeradores como  .
. - Por ser los términos impares los negativos multiplicamos por
 .
. - Finalmente, encontramos la expresión general:

b Encontrar el término general de la sucesión:
- El numerador es una progresión aritmética, con
 , es decir, la diferencia entre los numeradores consecutivos es
, es decir, la diferencia entre los numeradores consecutivos es  , por lo cual podemos expresar los numeradores como
, por lo cual podemos expresar los numeradores como  .
. - El numerador es una progresión geométrica, con
 , es decir, cada término en la sucesión es el doble que el anterior, por lo cual podemos expresar los numeradores como
, es decir, cada término en la sucesión es el doble que el anterior, por lo cual podemos expresar los numeradores como  .
. - Finalmente, encontramos la expresión general:

c Encontrar el término general de la sucesión: 
- Si prescindimos del signo, el numerador es una progresión aritmética con una
 . Por lo cual podemos expresar los numeradores como
. Por lo cual podemos expresar los numeradores como 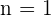 .
. - El denominador es una progresión geométrica con una
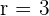 , además notemos que el primer término de la sucesión no empieza en un múltiplo de tres, por lo cual podemos expresar la sucesión de los denominadores como
, además notemos que el primer término de la sucesión no empieza en un múltiplo de tres, por lo cual podemos expresar la sucesión de los denominadores como  .
. - Por ser los términos impares los negativos multiplicamos por
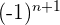 .
. - Finalmente, encontramos la expresión general:

2 Estudia la monotonia, la convergencia o divergencia y las cotas (si existen) de la siguiente sucesión 
- Recordemos que una sucesión es monótona creciente si cada término es menor o igual que el siguiente y monótona decreciente si cada término es menor o igual que el siguiente. Para determinar el comportamiento de la sucesión consideremos algunos términos:



- Como los términos aumentan entonces la sucesión es monótona estrictamente creciente.
b Sobre la convergencia o divergencia:
- El límite de la sucesión es
 es decir:
es decir:

- Por lo cual la sucesión es convergente.
c Sobre las cotas:
- Está acotada inferiormente, el mínimo es
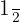 , cuando
, cuando  .
. - Está acotada superiormente pero no hay máximo el supremo es
 .
. - Por tanto la sucesión está acotada.

3 Hallar la fracción genaratriz de 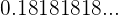
Podemos reescribir la fracción de la siguiente manera:
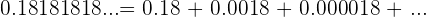
Notemos que es una progresión geométrica decreciente ilimitada, con las siguientes características:
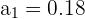
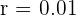
Después podemos utilizar la fórmula para calcular la fracción:
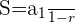

4 Juan ha comprado 20 libros, por el primero ha pagado un euro, por el segundo ha pagado dos euros, por el tercero ha pagado cuatro euros, por el cuarto ha pagado ocho euros y así sucesivamente. ¿Cuánto ha pagado por los libros?
En este caso, tenemos una progresión, donde los términos dados son: 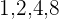 . Como podemos observar cada cantidad es el doble de la anterior, podemos deducir los siguientes datos:
. Como podemos observar cada cantidad es el doble de la anterior, podemos deducir los siguientes datos:
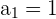


Donde 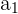 , es el valor del primer libro,
, es el valor del primer libro,  el factor de la progresión y
el factor de la progresión y  el número de libros.
el número de libros.
 Entonces lo que pagó es
Entonces lo que pagó es 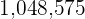 de euros.
de euros.5 Calcula tres números en progresión aritmética, que suman 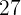 y siendo la suma de sus cuadrados
y siendo la suma de sus cuadrados  .
.
Por la primera hipótesis del problema sabemos que los tres número en progresión aritmética suman  . Es decir, a cada número de la progresión se le suma un factor constante
. Es decir, a cada número de la progresión se le suma un factor constante  . Es decir:
. Es decir:
- Si consideramos el segundo término como
 ,
, - el tercer término es
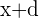 y
y - el primer término es

Ahora, podemos calcular la suma y encontrar el valor de  :
:
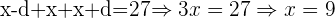
Para calcular el valor del primer y tercer término necesitamos conocer el valor de d. Usaremos la hipótesis de que la suma de sus cuadrados es  .
.

Desarollamos los binomios al cuadrado:
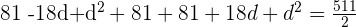
Simplificamos la expresión:
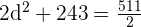
Multiplicamos ambos lados de la igualdad por  :
:

Resolvemos la ecuación:

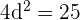
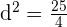

De tal forma que si  , entonces los términos son:
, entonces los términos son:  , notemos que si consideramos
, notemos que si consideramos  obtendremos los mismos valores pero ordenados de forma distinta.
obtendremos los mismos valores pero ordenados de forma distinta.
6 Uniendo los puntos medios de los lados de un cuadrado de lado  , se obtiene otro, en el que volvemos a hacer la misma operación, y así se continua indefinidamente. Calcular la suma de las áreas de los infinitos cuadrados.
, se obtiene otro, en el que volvemos a hacer la misma operación, y así se continua indefinidamente. Calcular la suma de las áreas de los infinitos cuadrados.
- Notemos que el área del primer cuadrado es
 .
. - Notemos que área del segundo cuadrado es
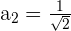 , lo anterior calculando la longitud de lado usando el teorema de Pitágoras:
, lo anterior calculando la longitud de lado usando el teorema de Pitágoras:  , como se ilustra en la siguiente gráfica:
, como se ilustra en la siguiente gráfica:

- De tal manera que si continuamos calculando los valores de las áreas tendremos la siguiente sucesión:
 . Así cualquier término es de la forma
. Así cualquier término es de la forma 
- Por la forma de la sucesión, la progresión es la siguiente:

Si tienes dudas puedes consultar la teoría



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
La suma.de los 9 primeros términos de una progresión es 219, si el primer término de la progresión es -4, habllar el último término An.
Son todos los tiempos de sucesiones?
No es clara tu pregunta, si te refieres a los ejercicios de inversión y depende del problema planteado.
Tres números x y z forman una progresión geométrica creciente que cumple x + y + z = 21 y x por y por z = 2 16 determina la razón de la progresión dada
Cuál es el número de término de una progresión aritmética cuando la diferencia común de los términos en 5,el primer término es 1 y el último es 46
En una PG a9 =56yr =1 , hallar a6
2
Encuentra el 6to,8vo,10mo termino de la siguiente sucesión geometrica3,6,12,14
Una progresión geométrica de razón positiva consta de 4 terminos
Porfa alguien me puede ayudar a comprender como puedo resolver un ejercisio sobre Sumar todos los términos de la progresión
1,34, 916, 2764, … y ando mas perdidaa