Arrastra cada progresión aritmética al cuadro que corresponda:
1




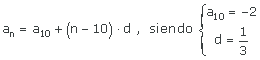
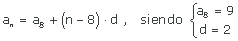
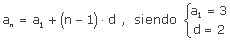

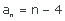 | 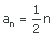 | 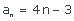 | 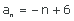 |
| (an) = (−3, −2, −1, 0, 1, ...) | (an) = (1/2, 1, 3/2, 2, 5/2, ...) | (an) = (1, 5, 9, 13, 17, ...) | (an) = (5, 4, 3, 2, 1, ...) |
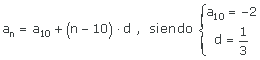 | 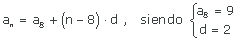 | 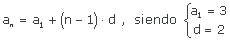 | 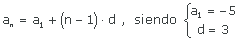 |
| (an) = (−5, −14/3, −13/3, −4, ...) | (an) = (−5, −3, −1, 1, 3, ...) | (an) = (3, 5, 7, 9, 11, ...) | (an) = (−5, −2, 1, 4, 7, ...) |
Di si las siguientes progresiones son aritméticas o no:
2La sucesión 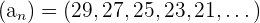 es una progresión aritmética.
es una progresión aritmética.
Recordemos que una progresión aritmética es una sucesión de números tales que cada uno de ellos (salvo el primero) es igual al anterior más un número fijo  .
.
Es decir, tendremos que en una progresión aritmética  se cumple que
se cumple que
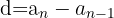
Veamos los elementos de la sucesión anterior

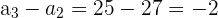


Por lo tanto sí es aritmética y su distancia es  .
.
3La sucesión  es una progresión aritmética.
es una progresión aritmética.
Notemos que

y además
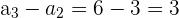
Al ser la distancia diferente en ambos casos, podemos concluir que no es aritmética.
4La sucesión  es una progresión aritmética.
es una progresión aritmética.
Nuevamente, observemos que

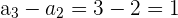
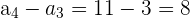
Es decir, no es aritmética.
5La sucesión  es una progresión aritmética.
es una progresión aritmética.
Veamos primeramente si se trata de una progresión aritmética
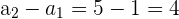
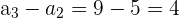


Tenemos que sí es aritmética y su distancia es 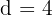 .
.
Ahora bien, recordemos que si conocemos el primer termino de la sucesión el término general está dado por la fórmula

Por tanto, en este caso el termino general es

Completa con lo que se pida en cada caso:
6 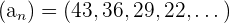 ,
,
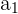 =
=
 =
=
Tenemos que

y para la distancia

7 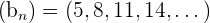 ,
,
 =
=
Tenemos que su primer termino es

y su distancia es
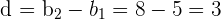
entonces su termino general es
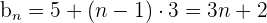
8  ,
,
 =
=
 =
=
Tenemos que su primer termino es
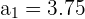
y su distancia es

entonces su termino general es
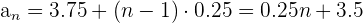
Usando su termino general tendremos que

9  ,
,
 =
=
Su distancia es
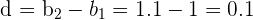
Por tanto, su termino general será

¿Necesitas clases particulares matematicas universidad? ¡Encuéntralas en Superprof!
Escribe el término general de las siguientes progresiones aritméticas conociendo los datos indicados de cada una:
10 ,
,
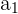 =
=
 =
=
Recordemos que si conocemos el valor que ocupa cualquier otro término de la progresión. El término general está dado por la fórmula
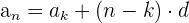
Por lo tanto,
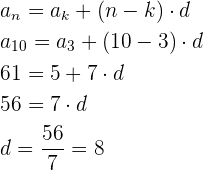
Después

Por tanto, el término general viene dado por:

11 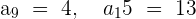 ,
,
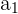 =
=
 =
=
Puesto que
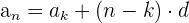
entonces

Ya con la distancia calculamos el primer termino
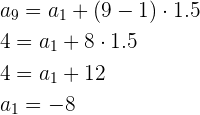
Por tanto, el término general viene dado por:

12 
 =
=
 =
=
Tenemos que

Después calculamos el primer termino
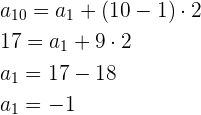
Por tanto

13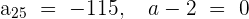
 =
=
 =
=
Comenzamos calculando la distancia 

Después obtenemos el primer termino de la sucesión
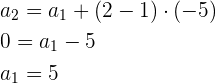
Por tanto, obtenemos que

Completa sabiendo que los números son términos de progresiones aritméticas:
Recordemos que interpolar medios diferenciales o aritméticos entre dos números, es construir una progresión aritmética que tenga por extremos los números dados.
Sean los extremos  y
y  , y el número de medios a interpolar
, y el número de medios a interpolar  . La diferencia está dada por:
. La diferencia está dada por:

En este caso los extremos son  y
y  , y el numero de medios son
, y el numero de medios son 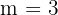 por tanto
por tanto

Tomando  , tendremos los términos de la sucesión de la siguiente manera
, tendremos los términos de la sucesión de la siguiente manera

En este caso los extremos son  y
y  , y el numero de medios son
, y el numero de medios son  por tanto
por tanto

Tomando  , tendremos los términos de la sucesión de la siguiente manera
, tendremos los términos de la sucesión de la siguiente manera
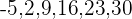
Los extremos son  y
y  , y el numero de medios son
, y el numero de medios son  por tanto
por tanto

Tomando  , tendremos los términos de la sucesión de la siguiente manera
, tendremos los términos de la sucesión de la siguiente manera

Los extremos son  y
y  , y el numero de medios son
, y el numero de medios son  por tanto
por tanto

Tomando  , tendremos los términos de la sucesión de la siguiente manera
, tendremos los términos de la sucesión de la siguiente manera

¿Buscas un profesor online de matematicas? ¡Encuéntralo en Superprof!
Realiza las siguientes sumas de términos consecutivos de progresiones aritméticas:
18Calcula la suma de los primeros siete términos de la progresión aritmética  ,
,
 =
=
Puesto que la distancia es
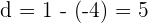
los siete primeros términos de la sucesión indicada son:
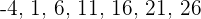
Ahora bien, recordemos que la suma de  términos consecutivos de una progresión aritmética viene dado por la siguiente formula
términos consecutivos de una progresión aritmética viene dado por la siguiente formula

por tanto

19Calcula la suma de los primeros 4 términos de la sucesión  ,
,
 =
=
Los primeros términos de la sucesión son

Usando la formula del ejercicio anterior

20 ¿Cuál es la suma de los primeros 100 números naturales?
 =
=
Los primeros 100 números naturales son los primeros cien términos de la progresión aritmética

Por tanto, usando la formula de obtenemos

Realiza el siguiente problema:
21Marco, Ana, José y Eva son hermanos que se llevan 3 años cada uno con su siguiente. Sus edades suman 38 años. Sabiendo que José tiene 11 años y que el orden en que se dan los nombres es de menor a mayor edad ¿sabrías decir la edad de cada uno de ellos?
Marco
Ana
José
Eva
Por llevarse cada hermano 3 años con su siguiente, podemos deducir que las edades se encuentran en progresión aritmética con distancia d = 3, luego podemos expresar las edades del siguiente modo:
Marcox años
Ana x + 3 años
José x + 6 = 11 años
Eva x + 9 años
Entonces, las edades son:
Marco5 años
Ana 8 años
José 11 años
Eva 14 años
Si tienes dudas puedes consultar la teoría



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
La suma.de los 9 primeros términos de una progresión es 219, si el primer término de la progresión es -4, habllar el último término An.
Son todos los tiempos de sucesiones?
No es clara tu pregunta, si te refieres a los ejercicios de inversión y depende del problema planteado.
Tres números x y z forman una progresión geométrica creciente que cumple x + y + z = 21 y x por y por z = 2 16 determina la razón de la progresión dada
Cuál es el número de término de una progresión aritmética cuando la diferencia común de los términos en 5,el primer término es 1 y el último es 46
En una PG a9 =56yr =1 , hallar a6
2
Encuentra el 6to,8vo,10mo termino de la siguiente sucesión geometrica3,6,12,14
Una progresión geométrica de razón positiva consta de 4 terminos
Porfa alguien me puede ayudar a comprender como puedo resolver un ejercisio sobre Sumar todos los términos de la progresión
1,34, 916, 2764, … y ando mas perdidaa