El límite de una sucesión es el número al cual se van aproximando los términos de una sucesión.
Veamos algunos ejemplos,
Ejemplos:
1 Consideremos los siguientes términos de una sucesión
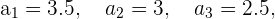
La sucesión es divergente y su límite es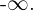 
2 Consideremos los siguientes términos de una sucesión
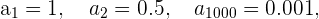
La sucesión se aproxima cada vez más a cero, podemos concluir que su límite es cero.
3 Veamos los siguientes términos de una sucesión de número positivos,
Estos términos nos indican que la sucesión esta tendiendo a 
. De hecho si continuamos viendo sus valores tendremos que su límite es realmente 
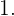
Una sucesión 
tiene por límite 
si y sólo si para cualquiera número positivo
que tomemos, existe un término 
, a partir del cual todos los términos de
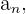siguientes a 
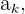cumplen que
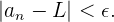
También podemos definir el límite de una sucesión mediante entornos:
Una sucesión tiene por límite si y sólo si para cualquier entorno de
que tomemos, por pequeño que sea su radio , existe un término de la sucesión, a
partir del cual, los siguientes términos pertenecen a dicho entorno.
Ejemplos:
1 Notemos que la sucesión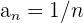 
tiene como límite cero.
Para esto tomemos un número muy cercano a cero, sea 
un número natural tal que
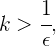
tenemos que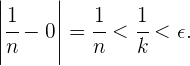
Lo cual nos indica que el límite es cero.
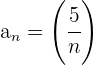es menor que 
?Consideremos algunos múltiplos de 
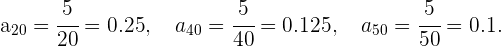y calculemos la sucesión para 
Para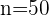 
tenemos que 
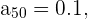lo cual implica que para número mayores a 
la sucesión es menor que . De hecho podemos ir notando que la sucesión es decreciente y que su límite es igual a cero.
3 ¿A partir de que número la sucesión
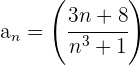
es menor que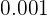 
?
Calculemos el valor de la sucesión para ciertos valores, digamos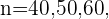 
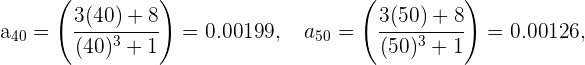
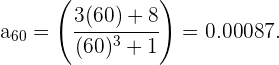
De esta forma podemos garantizar que a partir de 
se satisface la condición pedida. Más aún notemos que para 
la sucesión sigue disminuyendo,
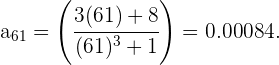
¿Buscas clases particulares matematicas universidad? ¡Están en Superprof!
Límite infinito de una sucesión
Una sucesión tiene por límite 
cuando para toda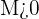 
existe un término , a partir del cual todos los términos de , siguientes a
cumplen que 
Una fórmula matemática que describe esto, es la siguiente
1 El límite de la sucesión 
es 
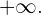
Calculemos algunos valores de la sucesión.
Para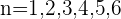 
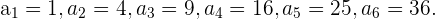
Para cualquier número natural 
podemos tomar 
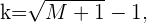así concluimos quepara cualquier se tiene que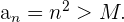 
Lo cual nos dice que el límite es infinito.
Finalmente, una sucesión tiene por límite 
cuando para toda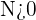 
existe un término , a partir del cual todos los términos de , siguientes a cumplen que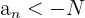 
.
2 El límite de la sucesión 
es .
Calculemos algunos valores de la sucesión. Para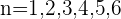
Para cualquier número natural 
podemos tomar 
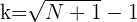, así concluimos que para cualquier se tiene que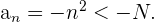 
Lo cual nos dice que el límite es menos infinito.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
La suma.de los 9 primeros términos de una progresión es 219, si el primer término de la progresión es -4, habllar el último término An.
Son todos los tiempos de sucesiones?
No es clara tu pregunta, si te refieres a los ejercicios de inversión y depende del problema planteado.
Tres números x y z forman una progresión geométrica creciente que cumple x + y + z = 21 y x por y por z = 2 16 determina la razón de la progresión dada
Cuál es el número de término de una progresión aritmética cuando la diferencia común de los términos en 5,el primer término es 1 y el último es 46
En una PG a9 =56yr =1 , hallar a6
2
Encuentra el 6to,8vo,10mo termino de la siguiente sucesión geometrica3,6,12,14
Una progresión geométrica de razón positiva consta de 4 terminos
Porfa alguien me puede ayudar a comprender como puedo resolver un ejercisio sobre Sumar todos los términos de la progresión
1,34, 916, 2764, … y ando mas perdidaa