Temas
¿Buscas un profesor matematicas?
Se llama sucesión a un conjunto de números dispuestos uno a continuación de otro:
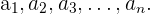
Los números 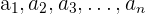 ; se llaman términos de la sucesión.
; se llaman términos de la sucesión.
El subíndice indica el lugar que el término ocupa en la sucesión.
El término general  es un criterio que nos permite determinar cualquier término de la
es un criterio que nos permite determinar cualquier término de la
sucesión.

Límite de una sucesión
Límite finito
Se dice que una sucesión  tiene por límite
tiene por límite  si y sólo si para cualquiera número positivo
si y sólo si para cualquiera número positivo 
que tomemos, existe un término  , a partir del cual todos los términos de
, a partir del cual todos los términos de  , siguientes a
, siguientes a
 cumplen que
cumplen que
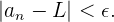
Es decir,
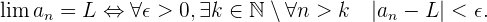
También podemos definir el límite de una sucesión mediante entornos:
Se dice que una sucesión  tiene por límite
tiene por límite  si y sólo si para cualquier entorno de
si y sólo si para cualquier entorno de  que
que
tomemos, por pequeño que sea su radio  , existe un término de la sucesión, a partir del cual,
, existe un término de la sucesión, a partir del cual,
los siguientes términos pertenecen a dicho entorno.
Si 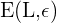 representa un entorno de
representa un entorno de  de radio
de radio  , entonces
, entonces

Límite infinito
Se dice que una sucesión  tiene por límite
tiene por límite  cuando para toda
cuando para toda 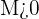 existe un
existe un
término  , a partir del cual todos los términos de
, a partir del cual todos los términos de  , siguientes a
, siguientes a  cumplen que
cumplen que
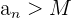 .
.
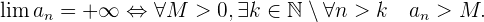
Se dice que una sucesión  tiene por límite
tiene por límite  cuando para toda
cuando para toda 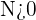 existe un
existe un
término  , a partir del cual todos los términos de
, a partir del cual todos los términos de  , siguientes a
, siguientes a  cumplen que
cumplen que
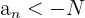 .
.
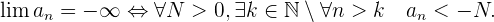
Propiedades de los límites
¿Necesitas clases de matematicas o clases algebra en Las Palmas?
La siguiente lista describe las propiedades usuales de los límites
1 Si el límite existe, entonces es único.
2 Si una sucesión  tiene límite, todas las subsucesiones tienen el mismo límite que
tiene límite, todas las subsucesiones tienen el mismo límite que  .
.
3 Todas las sucesiones convergentes están acotadas.
4 Hay sucesiones acotadas que no son convergentes.
5 Todas las sucesiones monótonas y acotadas son convergentes.
6 Hay sucesiones convergentes que no son monótonas.
Infinitésimos
Una sucesión  es un infinitésimo si tiene por límite cero.
es un infinitésimo si tiene por límite cero.
La siguiente lista describe las propiedades usuales de los infinitésimos
Propiedades:
1 La suma de dos infinitésimos es un infinitésimo.
2 El producto de un infinitésimo por una sucesión acotada es un infinitésimo.
3 El producto de infinitésimos es un infinitésimo.
4 El producto de una constante por un infinitésimo es un infinitésimo.
5 Si una sucesión  converge a
converge a  , la sucesión
, la sucesión  es un infinitésimo.
es un infinitésimo.
6 Si una sucesión  es divergente, su inversa es un infinitésimo.
es divergente, su inversa es un infinitésimo.
¿Estás buscando clases de algebra basica? ¡Están en Superprof!
Operaciones con límites
La siguiente lista describe las operaciones usuales con límites
1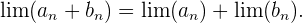
2
3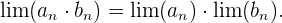
4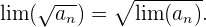
5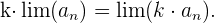
6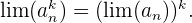
7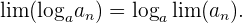
Al aplicarse estas propiedades pueden presentarse estos casos:
Hay que advertir que las expresiones simbólicas que utilizamos no son exactamente
igualdades, puesto que infinito no es número real, sino que es una forma convencional de
expresar resultados.
1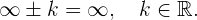
2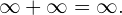
3
4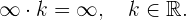
5
6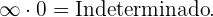
7
8
9
10
11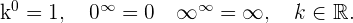
12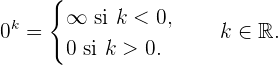
13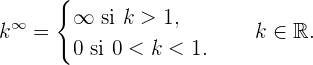
14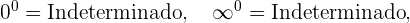
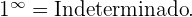
Determinación de una sucesión
Una sucesión se puede determinar de dos formas distintas las cuales presentamos a continuación
Por el término general
Podemos hallar un fórmula general para el  -ésimo término
-ésimo término  de la sucesión, por ejemplo
de la sucesión, por ejemplo
para la sucesión
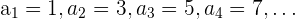
su término general es
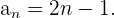
Por una ley de recurrencia
Los términos se obtienen operando con los anteriores. Por ejemplo para la sucesión,
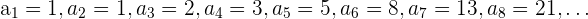
tenemos que
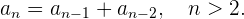
Operaciones con sucesiones
Dadas las sucesiones  ,
,  y
y  podemos definir las siguientes propiedades:
podemos definir las siguientes propiedades:

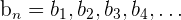
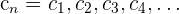
Suma con sucesiones
La suma de sucesiones se realiza término a término
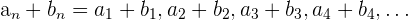
Propiedades
Así como en la suma usual de números tenemos las siguientes propiedades para la suma de sucesiones
1 Asociativa:

2 Conmutativa:
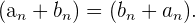
3 Elemento neutro
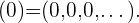
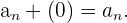
4 Sucesión opuesta
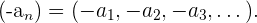

Diferencia con sucesiones
La diferencia de sucesiones se realiza término a término
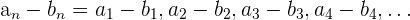
Producto con sucesiones
El producto de sucesiones se realiza término a término
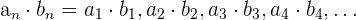
Propiedades
Así como en el producto usual de números tenemos las siguientes propiedades para el producto de sucesiones
1 Asociativa:

2 Conmutativa:
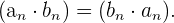
3 Elemento neutro

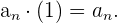
4 Sucesión inversa
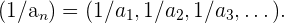
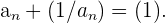
5 Distributiva respecto a la suma
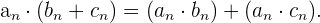
Sucesión inversible
Una sucesión es inversible o invertible si todos sus términos son distintos de
cero. Si la sucesión  es inversible, su inversa es:
es inversible, su inversa es:
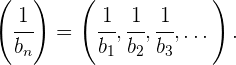
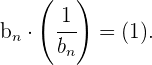
Cociente
Sólo es posible el cociente entre dos sucesiones si el denominador es
inversible.
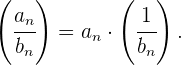
Tipos de sucesiones
Sucesiones monótonas
El siguiente diagrama nos muestra cada uno de los tipos de sucesiones monótonas que nos podemos encontrar

A continuación explicamos cada uno de ellos
Sucesiones estrictamente crecientes
Se dice que una sucesión es estrictamente creciente si cada término es mayor o
igual que el anterior.

Sucesiones crecientes
Se dice que una sucesión es creciente si cada término es mayor o igual que el
anterior.
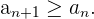
Sucesiones estrictamente decrecientes
Se dice que una sucesión es estrictamente decreciente si cada término de la
sucesión es menor que el anterior.
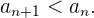
Sucesiones decrecientes
Se dice que una sucesión es estrictamente decreciente si cada término de la
sucesión es menor o igual que el anterior.
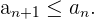
Sucesiones constantes
Se dice que una sucesión es constante si todos su términos son iguales a una
constante  , es decir,
, es decir,
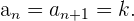
Sucesiones acotadas inferiormente
Una sucesión está acotada inferiormente si todos sus términos son mayores o
iguales que un cierto número  , que llamaremos cota inferior de la sucesión.
, que llamaremos cota inferior de la sucesión.

A la mayor de las cotas inferiores se le llama extremo inferior o ínfimo .
Si el ínfimo de una sucesión es uno de sus términos se le llama mínimo.
Toda sucesión acotada inferiormente es creciente.
Sucesiones acotadas superiormente
Una sucesión está acotada superiormente si todos sus términos son menores o
iguales que un cierto número 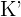 , que llamaremos cota superior de la sucesión.
, que llamaremos cota superior de la sucesión.
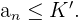
A la menor de las cotas superiores se le llama extremo superior o supremo.
Si el supremo de una sucesión es uno de sus términos se llama máximo.
Toda sucesión acotada superiormente es monótona decreciente.
Sucesiones acotadas
Una sucesión se dice acotada si está acotada superior e inferiormente. Es decir
si hay un número  menor o igual que todos los términos de la sucesión y otro
menor o igual que todos los términos de la sucesión y otro 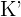
mayor o igual que todos los términos de la sucesión. Por lo que todos los
términos de la sucesión están comprendidos entre  y
y 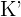 .
.

Sucesiones convergentes
Son las que tienen límite finito.
Sucesiones divergentes
Son las que tienen límite infinito  ó
ó  .
.
Sucesiones oscilantes
No son convergentes ni divergentes. Sus términos alternan de mayor a menor
o viceversa. Por ejemplo
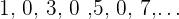
Sucesiones alternadas
Son aquellas que alternan los signos de sus términos.
Progresiones aritméticas
Una progresión aritmética es una sucesión de números tales que cada uno de
ellos (salvo el primero) es igual al anterior más un número fijo llamado diferencia
representada por  .
.
Término general de una progresión aritmética
Para una progresión de este estilo tenemos los siguientes tipos de término general
1 Si conocemos el 1er término.
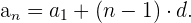
2 Si conocemos el valor que ocupa cualquier otro término de la progresión.

Interpolación de términos
Interpolar medios diferenciales o aritméticos entre dos números, es construir una
progresión aritmética que tenga por extremos los números dados.
Sean los  y
y  , y el número de medios a interpolar
, y el número de medios a interpolar  .
.
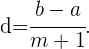
Suma de términos equidistantes
Sean 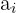 y
y  dos términos equidistantes de los extremos, se cumple que la suma
dos términos equidistantes de los extremos, se cumple que la suma
de términos equidistantes es igual a la suma de los extremos.
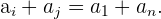
Dada la sucesión,

tenemos que
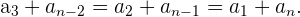
Suma de n términos consecutivos
La suma de  de una progresión aritmética se obtiene a través de la siguiente fórmula
de una progresión aritmética se obtiene a través de la siguiente fórmula
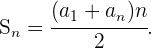
Progresiones geométricas
Una progresión geométrica es una sucesión en la que cada término se obtiene
multiplicando al anterior por una cantidad fija  , llamada razón.
, llamada razón.
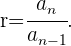
Término general de una progresión geométrica
Para una progresión de este estilo tenemos los siguientes tipos de término general
1 Si conocemos el 1er término.
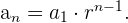
2 Si conocemos el valor que ocupa cualquier otro término de la progresión.

Interpolación de términos
Interpolar medios geométricos o proporcionales entre dos números, es construir
una progresión geométrica que tenga por extremos los números dados.
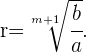
Suma de n términos consecutivos
La suma de  consecutivos de una progresión geométrica se obtiene a través de la siguiente fórmula
consecutivos de una progresión geométrica se obtiene a través de la siguiente fórmula

Suma de los términos de una progresión geométrica decreciente
Para el caso de una progresión geométrica decreciente tenemos la siguiente fórmula
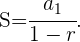
Producto de dos términos equidistantes
Sean 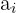 y
y  dos términos equidistantes de los extremos, se cumple que el
dos términos equidistantes de los extremos, se cumple que el
producto de términos equidistantes es igual al producto de los extremos.
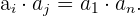
Dada la sucesión,

tenemos que
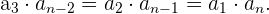
Producto de n términos equidistantes
En el caso de términos equidistantes el producto esta dado por
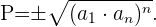
Término general de una sucesión
1 Comprobar si es una progresión aritmética.
2 Comprobar si es una progresión geométrica.
3 Comprobar si los términos son cuadrados perfectos.
También nos podemos encontrar con sucesiones cuyos términos son números
próximos a cuadrados perfectos.
4 Si los términos de la sucesión cambian consecutivamente de signo.
Si los términos impares son negativos y los pares positivos: Multiplicamos
 por
por  .
.
Si los términos impares son positivos y los pares negativos: Multiplicamos
 por
por 
5 Si los términos de la sucesión son fraccionarios (no siendo una
progresión).
Se calcula el término general del numerador y denominador por separado.
Estudio de las indeterminaciones
Infinito partido infinito
Se representa de la siguiente forma
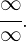
Solución: Se divide cada sumando por la potencia de mayor exponente.
Regla práctica
1 Si el numerador y denominador tienen el mismo grado, el límite es el
cociente entre los coeficientes de las potencias de mayor grado.
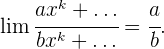

2 Si el denominador tiene mayor grado el límite es 0.
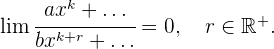
Infinito menos infinito
Se representa de la siguiente forma

1. Sucesión entera.
Se saca factor común de la potencia de mayor exponente.
Regla práctica:
El límite es  , dependiendo del signo del coeficiente de mayor grado.
, dependiendo del signo del coeficiente de mayor grado.
2. Sucesiones racionales.
Ponemos a común denominador, y si obtenemos  resolvemos la
resolvemos la
indeterminación.
3. Sucesiones irracionales.
Multiplicamos y dividimos por el conjugado.
Cero por infinito
Se representa de la siguiente forma
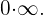
Se transforma a  .
.
Utilizando la siguiente igualdad
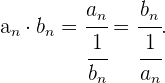
Cero partido por cero
Se representa de la siguiente forma
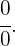
Se transforma a 
Uno elevado a infinito
Se representa de la siguiente forma
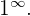
Se resuelve transformando la expresión en una potencia del número e .
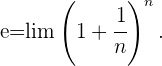
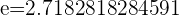
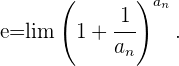
1er Método
Sumamos y restamos 1 en la base.
Ponemos a común denominador los últimos sumandos.
Sustituimos por el inverso del inverso.
Elevamos al denominador a su inverso.
2º Método
Dicha indeterminación se resuelve utilizando la siguiente igualdad
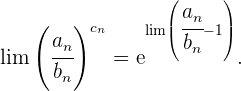
¿Buscas clases de matematicas en Vigo?













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
La suma.de los 9 primeros términos de una progresión es 219, si el primer término de la progresión es -4, habllar el último término An.
Son todos los tiempos de sucesiones?
No es clara tu pregunta, si te refieres a los ejercicios de inversión y depende del problema planteado.
Tres números x y z forman una progresión geométrica creciente que cumple x + y + z = 21 y x por y por z = 2 16 determina la razón de la progresión dada
Cuál es el número de término de una progresión aritmética cuando la diferencia común de los términos en 5,el primer término es 1 y el último es 46
En una PG a9 =56yr =1 , hallar a6
2
Encuentra el 6to,8vo,10mo termino de la siguiente sucesión geometrica3,6,12,14
Una progresión geométrica de razón positiva consta de 4 terminos
Porfa alguien me puede ayudar a comprender como puedo resolver un ejercisio sobre Sumar todos los términos de la progresión
1,34, 916, 2764, … y ando mas perdidaa