Temas

Definición de logaritmos
Seguramente has estudiado ya las potencias y sabes que, por ejemplo:
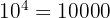
Pero, supongamos que quieres encontrar una potencia a la cual elevar al número 10 y que el resultado sea 10000000. Eso se puede escribir de la siguiente forma:
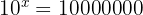
¿Podrías despejar la letra ' ' de dicha ecuación?
' de dicha ecuación?
La ecuación que escribimos es una ecuación exponencial. Para poder despejar la variable ' ' requerimos utilizar un logaritmo. Un logaritmo es una "operación" o "función" que te devuelve la potencia a la que debes elevar una base dada para obtener un resultado deseado. En nuestro ejemplo, la base es 10 y el resultado deseado es 10000000, por lo que podemos escribir que:
' requerimos utilizar un logaritmo. Un logaritmo es una "operación" o "función" que te devuelve la potencia a la que debes elevar una base dada para obtener un resultado deseado. En nuestro ejemplo, la base es 10 y el resultado deseado es 10000000, por lo que podemos escribir que:
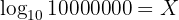
De manera general, podemos expresar la notación logarítmica de la siguiente forma:
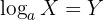
donde:
a es la base
x es el resultado deseado (también conocido como argumento)
y es la potencia a la que se eleva la base a
A continuación, te mostramos algunos ejemplos de expresiones en notación exponencial y notación logarítmica:
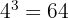

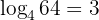
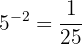

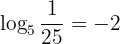


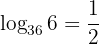
 y
y  (Número de Euler,
(Número de Euler, 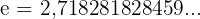 )
)Cuando usamos base  no es necesario escribir la base del logaritmo:
no es necesario escribir la base del logaritmo:
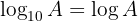
Al logaritmo con base  se le conoce como logaritmo neperiano (o logaritmo natural) y se representa así:
se le conoce como logaritmo neperiano (o logaritmo natural) y se representa así:

Propiedades de los logaritmos
1 El logaritmo de un producto es igual a la suma de los logaritmos de los factores
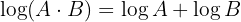
2 El logaritmo de un cociente es igual a la diferencia del logaritmo del dividendo y el logaritmo del divisor
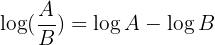
3 El logaritmo de una potencia es igual al producto del exponente por el logaritmo de la base
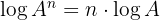
4El logaritmo de una raíz es igual al cociente entre el logaritmo del radicando y el índice de la raíz
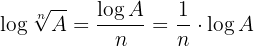
De las propiedades  y
y  podemos deducir que:
podemos deducir que:

5 El logaritmo base ' ' de '
' de ' ' es '
' es ' '
'
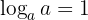
6 El logaritmo de  es
es  (Sin importar la base del logaritmo)
(Sin importar la base del logaritmo)
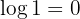
Por lo tanto:
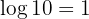
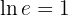
7 El argumento de un logaritmo siempre debe ser mayor que cero
Para  se cumple que
se cumple que 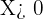
Uso de las propiedades de los logaritmos
Cambios de base
Para escribir un logaritmo de base ' ' en una expresión equivalente con logaritmo de base '
' en una expresión equivalente con logaritmo de base ' ' podemos realizar lo siguiente:
' podemos realizar lo siguiente:
Sea
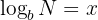
Podemos reescribir la expresión en su notación exponencial como:
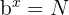
Aplicando 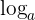 en ambos lados de la igualdad:
en ambos lados de la igualdad:
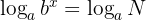
Aplicando la propiedad  y despejando a '
y despejando a ' ' obtenemos:
' obtenemos:
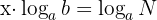

Por lo que:

Ejemplo: Reescribe el  en
en 
Aplicando: 
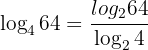
Resolver una expresión con operaciones combinadas aplicando las propiedades de los logaritmos
Ejemplo: Resuelve la operación 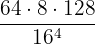 aplicando las propiedades de los logaritmos.
aplicando las propiedades de los logaritmos.
Igualemos a ' ' la expresión que queremos resolver:
' la expresión que queremos resolver:
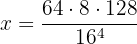
Como todos los números son potencias de  , podemos aplicar
, podemos aplicar  en ambos lados:
en ambos lados:

Aplicando las propiedades de los logaritmos del lado derecho obtenemos:
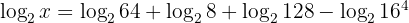
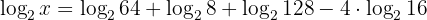
Resolviendo los logaritmos:

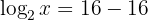
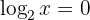
Reescribiendo en notación exponencial:


Por lo que:
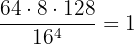
Escribir una expresión que contiene operaciones con logaritmos como una expresión que contenga un sólo logaritmo
Ejemplo: Escribe la siguiente operación con logaritmos como una expresión con un solo logaritmo

Aplicando las propiedades de los logaritmos:

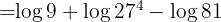

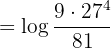













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Ayuda por favor con un logaritmo
Log3 (10-×) – log3 (3×-2) =2.
(√2+1)^X+(√2-1)^X=6
Puedes ayudarme?
Gracias
Hola muy buenos días me ayudaría con este ejercicio
(a²-1÷b)^n(a-1÷b)^-2n ÷(b²-1÷a²)-n(b+1÷a)^2n
3log(6-x)-log(72-x^3)=0