Capítulos
Introducción de los sistemas de ecuaciones logarítmicas
Para resolver sistemas de ecuaciones logarítmicas actuaremos de modo similar a como lo hicimos con las ecuaciones logarítmicas, es decir, basándonos en:
1 Definición de logaritmo:
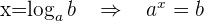
2 Inyectividad del logaritmo:
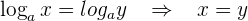
3 Propiedades de los logaritmos
Veamos dos casos de resolución de sistemas de ecuaciones logarítmicas.
Primer caso de sistema de ecuaciones logarítmicas
En la segunda ecuación aplicamos la propiedad del cociente de un logaritmo, en el primer miembro y en segundo tenemos en cuenta que el logaritmo decimal de 
es 
.
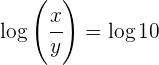
Resolvemos el sistema por sustitución
Aplicamos la inyectividad de los logaritmos
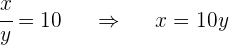
Sustituimos en la primera ecuación
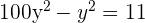
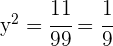
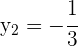
La solución 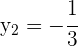no es válida porque tendríamos el logaritmo de un número negativo en la segunda ecuación
Al sustituir en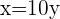 
obtenemos:
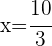
Segundo caso de sistema de ecuaciones logarítmicas
Algunos sistemas se pueden resolver directamente por el método de reducción.
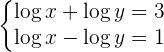
Sumando las dos ecuaciones obtenemos
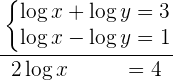
Aplicamos la definición de logaritmo
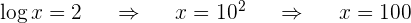
Sustituimos en la otra ecuación
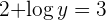
Aplicamos la definición de logaritmo
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
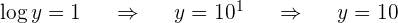
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
310=902,5/8,69ª
Quiero despejar a de allí
Es unpoco largo, es confuso vuando pone laprimera definicion logaX=Y, y dice que X es la ingonita. log aY=X lo expresa mejor
Hola agradecemos tu comentario pues nos ayuda a ser mas claros al explicar, vamos a analizar tu sugerencia para hacer los cambios necesarios.
-6(-×+3)/2
Cómo se puede resolver en esta situación?
Del logaritmo cuando se encuentra en fracciones
Hola depende del problema si es el logaritmo de una fracción (log(a/b)) se aplica una propiedad, si es una fracción de logaritmos (loga)/(logb) entonces se tiene que usar otros recursos que ten den en el ejercicio, espero poder haberte ayudado.
Hola el ejercicio no esta mal, pero tu tampoco estas mal porque 2/100=1/50 ya que la mitad de 2 es 1 y la de 100 es 50, son fracciones equivalentes, entonces la solución 2/100 no esta reducida.