Capítulos
¿Qué son las ecuaciones exponenciales?
Las ecuaciones exponenciales son aquellas en las que la variable se encuentra en el exponente de un número.
Por ejemplo:
Siendo 
y 
constantes
Para resolver las ecuaciones exponenciales, en general, nos encontraremos con dos casos: ecuaciones cuyos miembros puedan expresarse en una sola base y ecuaciones cuyos miembros NO puedan expresarse en una sola base. Aunque hay ecuaciones exponenciales en las que debemos emplear algún artilugio matemático para resolverlas.
Ecuaciones cuyos miembros pueden expresarse en una sola base
Para resolver este tipo de ecuaciones expresaremos los dos miembros de la ecuación en función de la misma base y luego igualamos los exponentes. Finalmente, resolvemos la ecuación que se obtenga al igualar los exponentes
Ecuaciones cuyos miembros NO pueden expresarse en una sola base
Para resolver estás ecuaciones, emplearemos logaritmos y sus propiedades para que la incógnita no quede en la potencia y posteriormente resolveremos la ecuación resultante
Otros tipos de ecuaciones exponenciales
Existen ecuaciones exponenciales en las que debemos emplear algunos artilugios matemáticos para poder despejar la variable
Ejercicios de ecuaciones exponenciales cuyos miembros pueden expresarse en una sola base
Resolver las siguientes ecuaciones exponenciales
1 Ya que el número 
puede escribirse como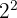 
, podemos reescribir la ecuación como:
2 Ya que tenemos base 
en ambos miembros de la ecuación, podemos igualar las potencias
3 Resolvemos la ecuación de primer grado que resultó
1 Transformamos las raíces en potencias de exponente fraccionario e igualamos los exponentes
2 Resolvemos la ecuación resultante
1 Reescribimos el 
como 
e igualamos los exponentes
2 Resolvemos la ecuación resultante
1 Reescribimos la raíz en forma de potencia de exponente fraccionario y el 
se descompone en factores
1Transformamos la fracción de la derecha
2 Igualamos exponentes y resolvemos la ecuación resultante
1 Transformamos las raíces en potencias de exponente fraccionario e igualamos los exponentes
2 Resolvemos la ecuación resultante
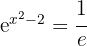
1 Reescribimos la fracción de la derecha
2 Igualamos exponentes y resolvemos la ecuación resultante
1Reescribimos la fracción del lado derecho y escribimos la raíz cuadrada como exponente fraccionario
2 Igualamos exponentes y resolvemos la ecuación resultante
1 Descomponemos en factores al y al 
e igualamos los exponentes
2 La ecuación resultante se puede simplificar y posteriormente se resuelve
1 Pasamos a la derecha al segundo término, descomponemos en factores al e igualamos los exponentes
2 Resolvemos la ecuación irracional que obtuvimos
Ejercicios de ecuaciones exponenciales cuyos miembros NO pueden expresarse en una sola base
Resolver las siguientes ecuaciones exponenciales
1 Como tenemos base distintas, aplicamos logaritmos en los dos miembros
2 Aplicamos la propiedad del logaritmo de una potencia en el primer miembro
3 Pasamos 
al otro miembro y resolvemos la ecuación
1 Podemos reescribir la ecuación como
2 Pasamos 
al primer miembro y al segundo miembro
3 Aplicamos logaritmo a los dos miembros
4 Aplicamos la propiedad del logaritmo de una potencia en el primer miembro y resolvemos la ecuación resultante
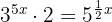
1 Podemos reescribir la ecuación como
2 Pasamos 
al primer miembro y al segundo miembro
3 Aplicamos logaritmo a los dos miembros
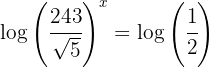
4 Aplicamos la propiedad del logaritmo de una potencia en el primer miembro y resolvemos la ecuación resultante
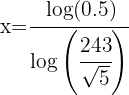
1 Aplicamos logaritmo a los dos miembros
2 Aplicamos la propiedad del logaritmo de una potencia en el primer miembro y resolvemos la ecuación resultante
1 Aplicamos logaritmo en los dos miembros y aplicamos la propiedad del logaritmo de un producto en el primer miembro
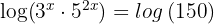
2 Aplicamos la propiedad del logaritmo de una potencia y sacamos factor común 
3 Despejamos la incógnita y resolvemos las operaciones con los logaritmos
Ejercicios de ecuaciones exponenciales mediante artilugios matemáticos
Resuelve las siguientes ecuaciones exponenciales
1 Aplicamos la propiedad de la potencia del producto y del cociente, para quitar la suma o la resta de los exponentes
2 Extraemos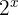 
como factor común
3 Despejamos 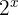y expresamos ambos miembros con base
4 Igualamos los exponentes
1 Aplicamos la propiedad de la potencia del cociente, para quitar la resta del exponente
2 Realizamos un cambio de variable y sustituimos en la ecuación
3 Al multiplicar ambos miembros de la ecuación por 
y pasando todos los términos al primer miembro obtenemos
4 Al resolver la ecuación cuadrática obtendríamos
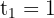
5 Sustituimos los valores de en
... 
... 
6 La ecuación no tiene solución, ya que una potencia con base positiva no puede dar un número negativo, así que resolvemos únicamente la ecuación
1 Aplicamos las propiedades de las potencias del producto o el cociente, para quitar las sumas o restas de los exponentes
2 Realizamos el cambio de variable y lo sustituimos en la ecuación
3 Multiplicamos ambos miembros por y resolvemos la ecuación resultante
No tiene solución
1 Descomponemos en factores, aplicamos las propiedades del producto y del cociente de potencias para quitar las sumas y restas de los exponentes
2 Realizamos el cambio de variable 
y resolvemos la ecuación resultante
3 Volvemos a la variable original y verificamos si las soluciones son válidas
No tiene solución
1 Descomponemos en factores al y al 
2 Realizamos el cambio de variable 
y resolvemos la ecuación resultante
3 Deshacemos el cambio de variable solo con la solución positiva.
4 Como no podemos igualar exponentes tomamos logaritmos en los dos miembros y en el primer miembro aplicamos la propiedad de la potencia
5 Despejamos la variable
6 Para la solución negativa de la ecuación cuadrática no obtendriamos solución para nuestra ecuación exponencial ya que al aplicar logaritmos en el segundo miembro nos encontraríamos con el logaritmo de un número negativo, que no existe.
No tiene solución
1 Quitamos exponentes negativos haciendo el inverso
2 Quitamos denominadores multiplicando por 
3 Realizamos el cambio de variable 
y resolvemos la ecuación resultante
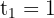
4 Regresamos a la variable original y resolvemos para
1 Realizamos el cambio de variable 
2 Resolvemos la ecuación y deshacemos el cambio de variable
No tiene solución
1 Aplicamos la fórmula de la suma de 
términos de una progresión geométrica
2 Despejamos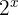
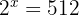
3 Reescribimos el 
como 
e igualamos las potencias
1 Aplicamos la fórmula de la suma de términos de una progresión geométrica
2 Ponemos los términos con común denominador
3 Quitamos denominadores y resolvemos la ecuación resultante
1 Elevamos al cubo ambos lados de la ecuación para que se mantenga la igualdad
2 Utilizamos las propiedades de los exponentes y reescribimos la ecuación. Usamos que 
3 Nuevamente, utilizamos las propiedades de los exponentes y reescribimos la ecuación
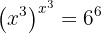
4 Por lo tanto tenemos que
5 Finalmente, tenemos que
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
-6(-×+3)/2
Cómo se puede resolver en esta situación?
Del logaritmo cuando se encuentra en fracciones
Hola depende del problema si es el logaritmo de una fracción (log(a/b)) se aplica una propiedad, si es una fracción de logaritmos (loga)/(logb) entonces se tiene que usar otros recursos que ten den en el ejercicio, espero poder haberte ayudado.
En el ejercicio 3, cuando reescribe la ecuacion pone 243^x , pero es 81^x.
3^4.
Muy buenos ejercicios, muchas gracias!
Hola el ejercicio ya fue corregido te agradecemos tu observación y una disculpa.
Hola el ejercicio no esta mal, pero tu tampoco estas mal porque 2/100=1/50 ya que la mitad de 2 es 1 y la de 100 es 50, son fracciones equivalentes, entonces la solución 2/100 no esta reducida.