1 Efectúa las siguientes operaciones con monomios:
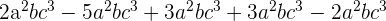
b
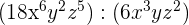 c
c 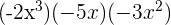 d
d 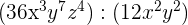 e
e 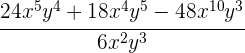
aSuma de términos semejantes, es decir, misma base y así solo sumamos o restamos los coeficientes

b División de monomios, recuerda que la ley de los exponentes es 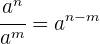 ,
,
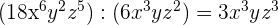
c Multiplicación de monomios, la ley de los exponentes nos dice 

d División de monomios, aplicamos la ley de los exponentes 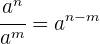 ,
,
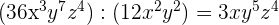
e En la siguiente división de polinomio entre monomio, separamos la suma y luego aplicamos la ley de los exponentes 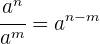 ,
,
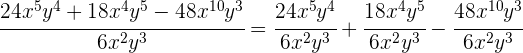

2 Dados los polinomios:
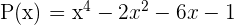
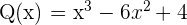
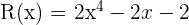
Calcular:
a 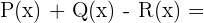
b 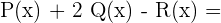
c 
Las operaciones aritméticas usuales, se siguen valiendo para las funciones, es decir, las sumas, restas y multiplicaciones por un escalar.
Comenzamos por sustituir el valor de cada función y efectuar las operaciones correspondientes.
a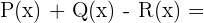
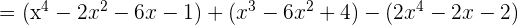

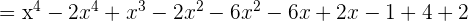
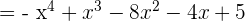
b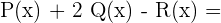

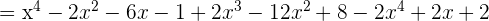


c
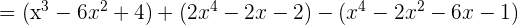

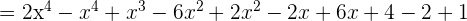
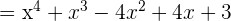
3 Calcula el valor de a, para que sea cierta la igualdad:


Quitamos los paréntesis
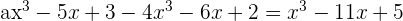
Agrupamos por términos semejantes
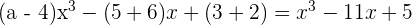
Realizamos las respectivas operaciones
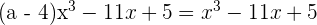
Podemos observar que casi tenemos la igualdad a excepción del primer término, entonces tenemos la siguiente igualdad, de dónde despejaremos el valor de a.
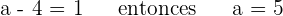
4 Multiplicar:
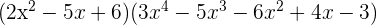
Recordemos que la multiplicación de polinomios es término a término.



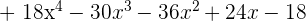
Agrupamos por términos semejantes para finalmenre llegar a la respuesta.
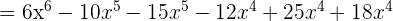
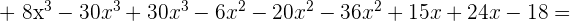
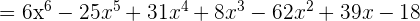
5 Divide:
a 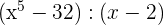
b 
a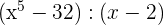
Para esta división utilizaremos el método de ruffini, suponiendo que  es una raíz exacta el resultado será el polinomio buscado de la división
es una raíz exacta el resultado será el polinomio buscado de la división



Entonces el polinomio resultante es
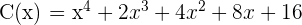
Y el residuo es 0

b 
Para este ejercicio ocuparemos la división sintética









Entonces el polinomio resultante es
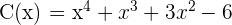
Y el residuo es

6 Calcula:
a 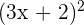
b 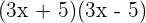
a 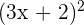

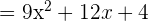
b 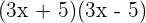

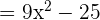



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
El valor númerico de la expresión 7(x²-2x+5)/3 , cuando x =-2
Hola, muchisimas gracias por compartir toda esta enseñanza. Mi duda es por que no me aparece la calificación si mi respuesta es tá acertada. Un saludo
El artículo que me aparece es:
10 ejercicios de polinomios 3 ESO I
Y en ese no sale calificación.
-12X-8-3X+10=2X-9+8Y
R=4n(n-a)+8n(a-n)-n(n-5a
(2x-1)(3x-5)-6x(2÷3x-1÷2)
10x + 2x