Temas
¡Bienvenidos a la sección de Ejercicios de Polinomios para estudiantes de 3º de Educación Secundaria Obligatoria (ESO)!
En este conjunto de ejercicios, exploraremos el mundo de los polinomios, que son expresiones algebraicas formadas por la suma o resta de términos llamados monomios. Los polinomios son herramientas fundamentales en álgebra y tienen diversas aplicaciones en la resolución de problemas matemáticos y en la representación de fenómenos en ciencias.
A lo largo de estos ejercicios, abordaremos conceptos clave como la identificación de términos semejantes, la suma y resta de polinomios, la multiplicación de polinomios y, en algunos casos, la factorización y división. Estos ejercicios están diseñados para fortalecer tu comprensión de los polinomios y mejorar tus habilidades en la manipulación algebraica.
Esperamos que disfrutes enfrentándote a estos desafíos y que encuentres la práctica que necesitas para consolidar tus conocimientos en el emocionante mundo de los polinomios. ¡Vamos a sumergirnos en la resolución de ejercicios y a explorar las propiedades y operaciones de estos expresivos objetos algebraicos!

Identificar monomios
Indica cuales de las siguientes expresiones son monomios. En caso afirmativo, indica su grado y coeficiente.
1 
2 
3 
4 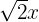
5 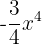
6 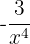
7 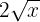
8 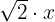
9 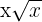
10 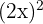
Indica cuales de las siguientes expresiones son monomios. En caso afirmativo, indica su grado y coeficiente.
1 
Si es un monomio; grado 3 y coeficiente 3.
2 
No es un monomio, porque el exponente no es un número natural.
3 
No es un monomio, porque aparece una suma.
4 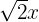
Si es un monomio; grado 1 y coeficiente 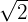 .
.
5 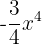
Si es un monomio; grado 4 y coeficiente 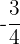 .
.
6 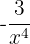
No es un monomio, no tiene exponente natural.
7 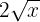
No es monomio, porque la parte literal está dentro de una raíz.
8 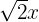
Si es monomio; grado 1 y coeficiente 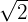 .
.
9 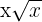
No es monomio, porque 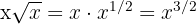 , que es un exponente no natural.
, que es un exponente no natural.
10 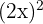
Si es monomio; de grado 2 y coeficiente 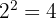 .
.
Operaciones con monomios
Efectúa las siguientes operaciones con monomios:
1 
2 
3 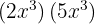
4 
5 
6 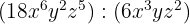
7 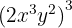
8 
9 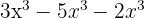
10 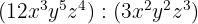
11 
12 
13 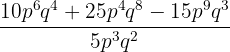
14 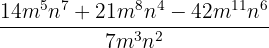
15 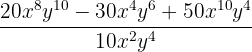
Efectúa las siguientes operaciones con monomios:
1 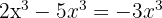
2 
3 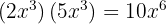
4 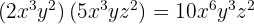
5 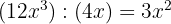
6 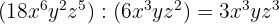
7 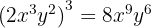
8 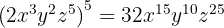
9 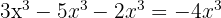
10 
11 
12 
13 
14 
15 
Identificar polinomios
Di si las siguientes expresiones algebraicas son polinomios o no. En caso afirmativo, señala cuál es su grado y término independiente.
1 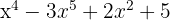
2 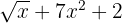
3 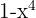
4 
5 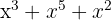
6 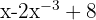
7 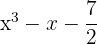
8 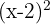
9 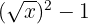
10 
Di si las siguientes expresiones algebraicas son polinomios o no. En caso afirmativo, señala cuál es su grado y término independiente.
1 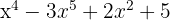
Si es polinomio; grado 5 y término independiente 5
2 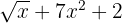
No es un polinomio, porque la parte literal del primer monomio está dentro de una raíz.
3 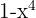
Si es polinomio; grado 4 y término independiente 1
4 
No es un polinomio, porque el exponente del primer monomio no es un número natural.
5 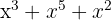
Si es polinomio; grado 5 y término independiente 0
6 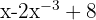
No es un polinomio, porque el exponente del segundo monomio no es un número natural.
7 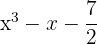
Si es polinomio; grado 3 y término independiente 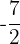
8 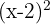
Si es polinomio; grado 2 y término independiente 
9 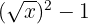
Si es polinomio; grado 1 y término independiente 
10 
No es polinomio, porque el exponente no es un número natural.
Escribir en lenguaje matemático
Escribe:
1Un polinomio ordenado sin término independiente.
2Un polinomio no ordenado y completo.
3Un polinomio completo sin término independiente.
4Un polinomio de grado 4, completo y con coeficientes impares.
5Un polinomio de grado 2, completo y con coeficientes negativos.
Escribe:
1Un polinomio ordenado sin término independiente.
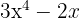
2Un polinomio no ordenado y completo.
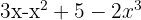
3Un polinomio completo sin término independiente.
Imposible
4Un polinomio de grado 4, completo y con coeficientes impares.
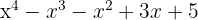
5Un polinomio de grado 2, completo y con coeficientes negativos.
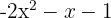
Cálculo con polinomios
Dados los polinomios:
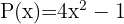



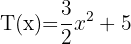

Calcular:
1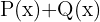
2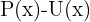
3
4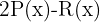
5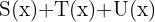
6
7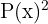
8
9
10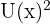
Dados los polinomios:
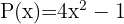



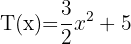

Calcular:
1
2 
3 
4 
5 
6 
7

8

9

10

Multiplicaciones
Multiplicar:
1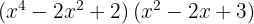
2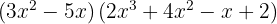
3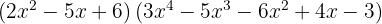
4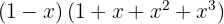
5
Multiplicar:
1
2
3
4

5

Hallar el valor numérico del polinomio
Hallar el valor numérico del polinomio  , para:
, para: 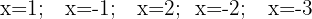 .
.
Hallar el valor numérico del polinomio  , para:
, para: 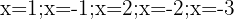 .
.
1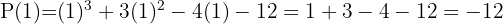
2
3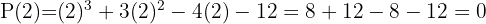
4
5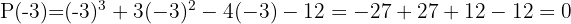
Cálculo
Calcula:
1
2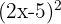
3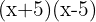
4
5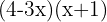
Calcula:
1
2
3
4
5

Division de polinomios
Dividir:
1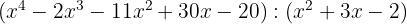
2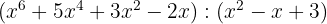
3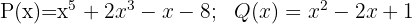
4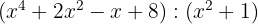
5
Dividir:
1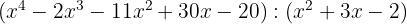

Cociente  ; Residuo
; Residuo 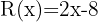
2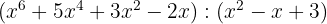

Cociente  ; Residuo
; Residuo 
3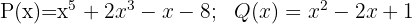

Cociente 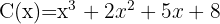 ; Residuo
; Residuo 
4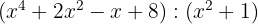

5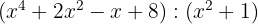

Division por Ruffini
Divide por Ruffini:
1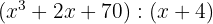
2
3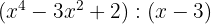
4
5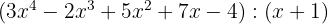
Divide por Ruffini:
1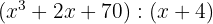

Cociente  ; Residuo
; Residuo 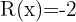
2

Cociente 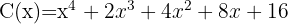 ; Residuo
; Residuo 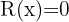
3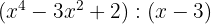

Cociente 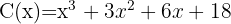 ; Residuo
; Residuo 
4

 con un residuo de -2.
con un residuo de -2.
5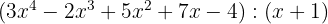

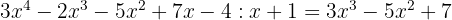 con un residuo de -11.
con un residuo de -11.













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
como encontrar las posibles raices de un polinomio si el termino independiente de la funcion es 1: X4 + 2×3 -6×2 +2x +1 = 0
El valor númerico de la expresión 7(x²-2x+5)/3 , cuando x =-2
Hola, muchisimas gracias por compartir toda esta enseñanza. Mi duda es por que no me aparece la calificación si mi respuesta es tá acertada. Un saludo
El artículo que me aparece es:
10 ejercicios de polinomios 3 ESO I
Y en ese no sale calificación.
-12X-8-3X+10=2X-9+8Y
R=4n(n-a)+8n(a-n)-n(n-5a
(2x-1)(3x-5)-6x(2÷3x-1÷2)
10x + 2x
Ayúdenme aquí (3m+n)+(m-2n)