Dados los polinomios




realiza las operaciones que se indican a continuación:
1 









2 (















3 

















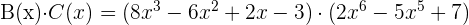


4 





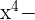









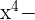



En el ejercicio anterior habíamos calculado  , por tanto:
, por tanto:



5 







 +
+ 








 +
+ 
Ordenamos  y calculamos en primer lugar
y calculamos en primer lugar  :
:



Multiplicamos por  :
:



Si tienes dudas puedes consultar la teoría



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
El valor númerico de la expresión 7(x²-2x+5)/3 , cuando x =-2
Hola, muchisimas gracias por compartir toda esta enseñanza. Mi duda es por que no me aparece la calificación si mi respuesta es tá acertada. Un saludo
El artículo que me aparece es:
10 ejercicios de polinomios 3 ESO I
Y en ese no sale calificación.
-12X-8-3X+10=2X-9+8Y
R=4n(n-a)+8n(a-n)-n(n-5a
(2x-1)(3x-5)-6x(2÷3x-1÷2)
10x + 2x