Temas

Definición del polinomio
Un monomio es una expresión algebraica conformada por un coeficiente, una variable (generalmente  ) y un exponente, por ejemplo:
) y un exponente, por ejemplo:
Un polinomio es una expresión algebraica formada por la suma de un número finito de monomios
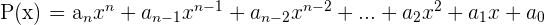
donde,  es un número natural y
es un número natural y
Coeficientes: 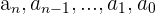
Variable o indeterminada: 
Coeficiente principal: 
Término independiente: 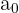
Ejemplo
Coeficientes: 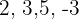
Variable o indeterminada: 
Coeficiente principal: 
Término independiente: 
Grado de un Polinomio
El grado de un polinomio P(x) es el mayor exponente al que se encuentra elevada la variable x
Según su grado los polinomios pueden ser de:
| TIPO | EJEMPLO |
| Grado cero | 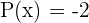 |
| Primer grado |  |
| Segundo grado |  |
| Tercer grado | 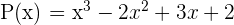 |
| Cuarto grado |  |
| Quinto grado | 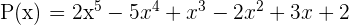 |
Tipos de polinomios
1 Polinomio nulo
Es aquel polinomio que tiene todos sus coeficientes nulos.
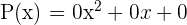
2 Polinomio homogéneo
Es aquel polinomio en el que todos sus términos o monomios son del mismo grado.

3Polinomio heterogéneo
Es aquel polinomio en el que no todos sus términos no son del mismo grado.

4 Polinomio completo
Es aquel polinomio que tiene todos los términos desde el término independiente hasta el término de mayor grado.
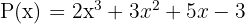
5 Polinomio incompleto
Es aquel polinomio que no tiene todos los términos desde el término independiente hasta el término de mayor grado.
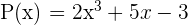
6 Polinomio ordenado
Un polinomio está ordenado si los monomios que lo forman están escritos de mayor a menor grado.
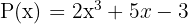
7 Polinomios iguales
Dos polinomios son iguales si verifican:
Los dos polinomios tienen el mismo grado.
Los coeficientes de los términos del mismo grado son iguales.
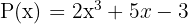

8 Polinomios semejantes
Dos polinomios son semejantes si verifican que tienen la misma parte literal.
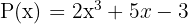
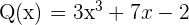
9Polinomio mónico
Un polinomio es mónico si su coeficiente principal es 1, por ejemplo

Monomio
Es un polinomio que consta de un sólo monomio.
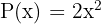
Binomio
Es un polinomio que consta de dos monomios.

Trinomio
Es un polinomio que consta de tres monomios.
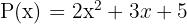
Valor numérico de un polinomio
El valor numérico de un polinomio es el resultado que obtenemos al sustituir la variable x por un número cualquiera.
Ejemplo:
Calcular el valor numérico del polinomio: 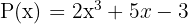 , para los valores
, para los valores
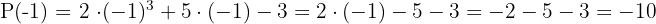

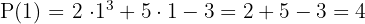
Polinomio de varias variables
Un polinomio puede tener varias variables. En este caso, los monomios, de manera análoga, cuetan con un coeficiente y varias variables cada una con un respectivo exponente. Por ejemplo
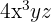
Ejemplos:


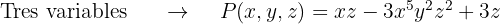
También se puede obtener el valor numérico de estos
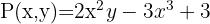
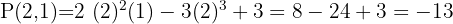
















Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
El valor númerico de la expresión 7(x²-2x+5)/3 , cuando x =-2
-12X-8-3X+10=2X-9+8Y
(2x-1)(3x-5)-6x(2÷3x-1÷2)
10x + 2x
Mesecito ayuda de matemáticas
Puedes obtenerla en https://www.superprof.es/ 🙂
Halla el cociente y el residuo de las divisiones siguientes
(.^3-3.^2+2.-2)\(.+1)
Alguien me ayuda en este problema de polinomios 1. P(x) = 7
2. Q(x) = 4x
2 − 1
3. R(x) = 2x
4 + 5
4. S(x) = x
5 + 2x
2 − 7
5. T(x) = 4x
6 + 2x
3 − 1
6. U(x) = 5x
8