Temas

Expresiones algebraicas
Trabajar en álgebra consiste en manejar relaciones numéricas en las que una o más cantidades son desconocidas. Estas cantidades se llaman variables, incógnitas o indeterminadas y se representan por letras.
Una expresión algebraica es una combinación de letras y números ligada por los signos de las operaciones: adición, sustracción, multiplicación, división y potenciación.
El valor numérico de una expresión algebraica es el número que se obtiene al sustituir las letras de la misma por números determinados y efectuar las operaciones indicadas en la expresión.
Monomios
Un monomio es una expresión algebraica en la que las únicas operaciones que aparecen entre las variables son el producto y la potencia de exponente natural.
El coeficiente del monomio es el número que aparece multiplicando a las variables.
La parte literal está constituida por las letras y sus exponentes.
El grado de un monomio es la suma de todos los exponentes de las letras o variables.
Dos monomios son semejantes cuando tienen la misma parte literal.
Si estás buscando un profesor de mates, ¡encuéntralo en Superprof!
Operaciones con monomios
Suma de Monomios
Sólo podemos sumar monomios semejantes.
La suma de los monomios es otro monomio que tiene la misma parte literal y cuyo coeficiente es la suma de los coeficientes.
Producto de un número por un monomio
El producto de un número por un monomio es otro monomio semejante cuyo coeficiente es el producto del coeficiente de monomio por el número.
Producto de monomios
El producto de monomios es otro monomio que tiene por coeficiente el producto de los coeficientes y cuya parte literal se obtiene sumando las potencias que tengan la misma base.
Cociente de monomios
El cociente de monomios es otro monomio que tiene por coeficiente el cociente de los coeficientes y cuya parte literal se obtiene restando las potencias que tenga la misma base.
Polinomios
Un polinomio es una expresión algebraica de la forma:
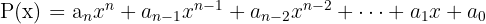
Siendo  números, llamados coeficientes.
números, llamados coeficientes.
 un número natural.
un número natural.
 la variable o indeterminada.
la variable o indeterminada.
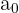 es el término independiente.
es el término independiente.
Grado de un polinomio
El grado de un polinomio  es el mayor exponente al que se encuentra elevada la variable
es el mayor exponente al que se encuentra elevada la variable  .
.
Polinomio completo
Es aquel que tiene todos los términos desde el término independiente hasta el término de mayor grado.
Polinomio ordenado
Un polinomio está ordenado si los monomios que lo forman están escritos de mayor a menor grado.
Polinomios iguales
Dos polinomios son iguales si verifican:
1Los dos polinomios tienen el mismo grado.
2Los coeficientes de los términos del mismo grado son iguales.
Valor numérico de un polinomio
Es el resultado que obtenemos al sustituir la variable  por un número cualquiera.
por un número cualquiera.
Operaciones con polinomios
Suma de polinomios
Para sumar dos polinomios se suman los coeficientes de los términos del mismo grado.
La diferencia consiste en sumar el opuesto del sustraendo.
Multiplicación de polinomios
Producto de un número por un polinomio
Es otro polinomio que tiene de grado el mismo del polinomio y como coeficientes el producto de los coeficientes del polinomio por el número.
Producto de un monomio por un polinomio
Se multiplica el monomio por todos y cada uno de los monomios que forman el polinomio.
Producto de polinomios
1 Se multiplica cada monomio del primer polinomio por todos los elementos segundo polinomio.
2 Se suman los monomios del mismo grado.
División de polinomios
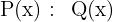
1 A la izquierda situamos el dividendo. Si el polinomio no es completo dejamos huecos en los lugares que correspondan.
2 A la derecha situamos el divisor dentro de una caja.
3 Dividimos el primer monomio del dividendo entre el primer monomio del divisor.
4 Multiplicamos cada término del polinomio divisor por el resultado anterior y lo restamos del polinomio dividendo:
5 Volvemos a dividir el primer monomio del dividendo entre el primer monomio del divisor. Y el resultado lo multiplicamos por el divisor y lo restamos al dividendo.
6 Repetimos el proceso anterior hasta que el grado del resto sea menor que el grado del divisor, y por tanto no se puede continuar dividiendo.
7 Para comprobar si la operación es correcta, utilizaríamos la prueba de la división:
Si necesitas ayuda con las mates, ¿por qué no pruebas a buscar un profesor matematicas online?
Regla de Ruffini
Si el divisor es un binomio de la forma 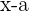 , entonces utilizamos un método más breve para hacer la división, llamado regla de Ruffini.
, entonces utilizamos un método más breve para hacer la división, llamado regla de Ruffini.

1Si el polinomio no es completo, lo completamos añadiendo los términos que faltan con ceros.
2Colocamos los coeficientes del dividendo en una línea.
3Abajo a la izquierda colocamos el opuesto del término independiente del divisor.
4Trazamos una raya y bajamos el primer coeficiente.

5Multiplicamos ese coeficiente por el divisor y lo colocamos debajo del siguiente término.
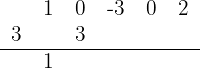
6Sumamos los dos coeficientes.
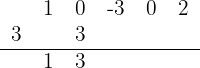
7Repetimos los pasos 5y 6las veces que fuera necesarias.
8El último número obtenido es el resto.
9El cociente es un polinomio de grado inferior en una unidad al dividendo y cuyos coeficientes son los que hemos obtenido.
Identidades notables
Binomio al cuadrado

Suma por diferencia
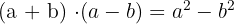
Binomio al cubo
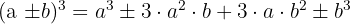
Factorización de un polinomio
Teorema del resto
El resto de la división de un polinomio  , entre un polinomio de la forma
, entre un polinomio de la forma  es el valor numérico de dicho polinomio para el valor:
es el valor numérico de dicho polinomio para el valor:  .
.
Teorema del factor
El polinomio  es divisible por un polinomio de la forma
es divisible por un polinomio de la forma  si y sólo si
si y sólo si 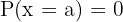 .
.
Al valor  se le llama raíz o cero de
se le llama raíz o cero de  .
.
Observaciones
1Los ceros o raíces son divisores del término independiente del polinomio.
2A cada raíz del tipo  le corresponde un binomio del tipo
le corresponde un binomio del tipo 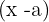 .
.
3 Podemos expresar un polinomio en factores al escribirlo como producto de todos los binomios del tipo  , que se correspondan a las raíces
, que se correspondan a las raíces  que se obtengan.
que se obtengan.
4La suma de los exponentes de los binomios ha de ser igual al grado del polinomio.
5Todo polinomio que no tenga término independiente admite como raíz  , ó lo que es lo mismo, admite como factor
, ó lo que es lo mismo, admite como factor  .
.
6Un polinomio se llama irreducible o primo cuando no puede descomponerse en factores.
Métodos para factorizar un polinomio
Factor común
Consiste en aplicar la propiedad distributiva.
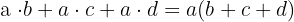
Diferencia de cuadrados
Una diferencia de cuadrados es igual a suma por diferencia.
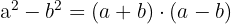
Trinomio cuadrado perfecto
Un trinomio cuadrado perfecto es igual a un binomio al cuadrado.
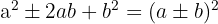
Trinomio de segundo grado
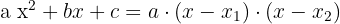
Polinomio de grado superior a dos
Utilizamos el teorema del resto y la regla de Ruffini.
1Tomamos los divisores del término independiente:  .
.
2Aplicando el teorema del resto sabremos para que valores la división es exacta.
3Dividimos por Ruffini.
4Por ser la división exacta, 
5Continuamos realizando las mismas operaciones al segundo factor, y los nuevos que obtengamos, hasta que sea de grado uno o no se pueda descomponer en factores reales.
Fracciones algebraicas
Una fracción algebraica es el cociente de dos polinomios y se representa por:
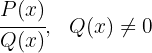
 es el numerador y
es el numerador y  el denominador.
el denominador.
Fracciones algebraicas equivalentes
Dos fracciones algebraicas
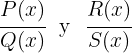
son equivalentes, y lo representamos por:

si se verifica que  .
.
Dada una fracción algebraica, si multiplicamos o dividimos el numerador y el denominador de dicha fracción por un mismo polinomio distinto de cero, la fracción algebraica resultante es equivalente a la dada.

Simplificación de fracciones algebraicas
Para simplificar una fracción algebraica se divide el numerador y el denominador de la fracción por un polinomio que sea factor común de ambos.
Reducción de fracciones algebraicas a común denominador
Dadas dos fracciones algebraicas, reducirlas a común denominador es encontrar dos fracciones algebraicas equivalentes con el mismo denominador.
1Descomponemos los denominadores en factores para hallarles el mínimo común múltiplo, que será el común denominador.
2Dividimos el común denominador entre los denominadores de las fracciones dadas y el resultado lo multiplicamos por el numerador correspondiente.
Operaciones con fracciones algebraicas
Suma y diferencia de fracciones algebraicas
Fracciones algebraicas con igual denominador
La suma de fracciones algebraicas con el mismo denominador es otra fracción algebraica con el mismo denominador y cuyo numerador es la suma de los numeradores.
Fracciones algebraicas con distinto denominador
En primer lugar se ponen las fracciones algebraica a común denominador, posteriormente se suman los numeradores.
Producto de fracciones algebraicas
El producto de dos fracciones algebraicas es otra fracción algebraica donde el numerador es el producto de los numeradores y el denominador es el producto de los denominadores.
Cociente de fracciones algebraicas
El cociente de dos fracciones algebraicas es otra fracción algebraica con numerador el producto del numerador de la primera por el denominador de la segunda, y con denominador el producto del denominador de la primera por el numerador de la segunda.













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
como encontrar las posibles raices de un polinomio si el termino independiente de la funcion es 1: X4 + 2×3 -6×2 +2x +1 = 0
El valor númerico de la expresión 7(x²-2x+5)/3 , cuando x =-2
Hola, muchisimas gracias por compartir toda esta enseñanza. Mi duda es por que no me aparece la calificación si mi respuesta es tá acertada. Un saludo
El artículo que me aparece es:
10 ejercicios de polinomios 3 ESO I
Y en ese no sale calificación.
-12X-8-3X+10=2X-9+8Y
R=4n(n-a)+8n(a-n)-n(n-5a
(2x-1)(3x-5)-6x(2÷3x-1÷2)
10x + 2x
Ayúdenme aquí (3m+n)+(m-2n)