Elige la opción correcta:
1Las raíces del polinomio 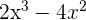 son...
son...
1 Para encontrar las raíces de polinomio tenemos que resolver
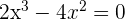
2 Factorizamos el polinomio
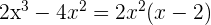
3 Para obtener las raíces igualamos cada factor a cero y despejamos
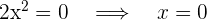

Así, las raíces son 0 y 2
2Las raíces del polinomio 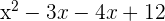 son...
son...
1 Para encontrar las raíces de polinomio tenemos que resolver

2 Simplificamos el polinomio

3 Factorizamos el polinomio
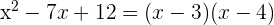
4 Para obtener las raíces igualamos cada factor a cero y despejamos
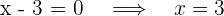
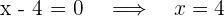
Así, las raíces son 3 y 4
3El polinomio  se factoriza como...
se factoriza como...
1 Para encontrar las raíces de polinomio tenemos que resolver
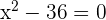
2 Factorizamos el polinomio
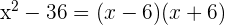
3 Para obtener las raíces igualamos cada factor a cero y despejamos


Así, las raíces son 6 y -6
4Las raíces del polinomio 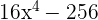 son...
son...
1 Para encontrar las raíces de polinomio tenemos que resolver
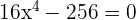
2 Factorizamos el polinomio
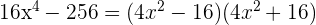
El segundo factor no puede factorizarse en los reales y no posee raíces, pero el primer factor si se puede factorizar
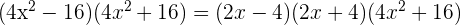
3 Para obtener las raíces igualamos cada factor a cero y despejamos. Recuerda que el factor 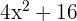 no posee raíces reales
no posee raíces reales
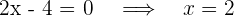
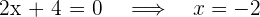
Así, las raíces son 2 y -2
5Las raíces de 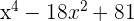 son...
son...
1 Para encontrar las raíces de polinomio tenemos que resolver

2 Factorizamos el polinomio
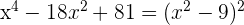
El interior del paréntesis puede ser factorizado

Así la factorización queda
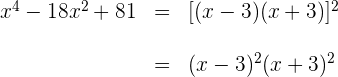
3 Para obtener las raíces igualamos cada factor a cero y despejamos. Recuerda que al tener los factores lineales potencia dos, las raíces serán dobles
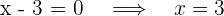
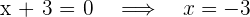
Así, las raíces son 3 y -3 y ambas son raíces dobles.
6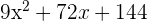 tiene como raiz...
tiene como raiz...
1 Para encontrar las raíces de polinomio tenemos que resolver

2 Factorizamos el polinomio
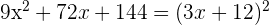
3 Para obtener las raíces igualamos el factor a cero
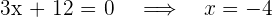
Así, la raiz es -4 es una raiz doble.
7 Las raíces del polinomio 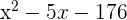 son...
son...
1 Para encontrar las raíces de polinomio tenemos que resolver

2 Factorizamos el polinomio
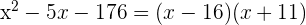
3 Para obtener las raíces igualamos los factores a cero

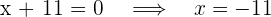
Así, las raices son 16 y -11
8Las raíces del polinomio  son...
son...
1 Para encontrar las raíces de polinomio tenemos que resolver

2 Factorizamos el polinomio
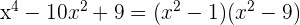
El interior de cada paréntesis puede ser factorizado
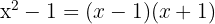

Así la factorización queda
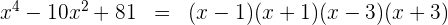
3 Para obtener las raíces igualamos cada factor a cero y despejamos
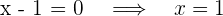
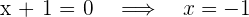
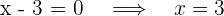
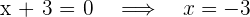
Así, las raíces son -1, 1, -3 y 3
9Las raíces del polinomio 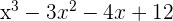 son...
son...
1 Para encontrar las raíces de polinomio tenemos que resolver
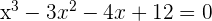
2 Factorizamos el polinomio
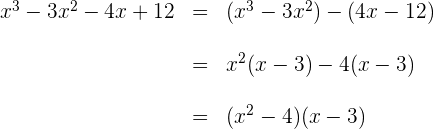
El interior del primer paréntesis puede ser factorizado
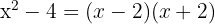
Así la factorización queda
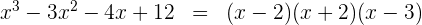
3 Para obtener las raíces igualamos cada factor a cero y despejamos

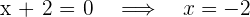
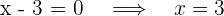
Así, las raíces son -2, 2 y 3
10Las raíces del polinomio 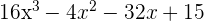 son...
son...
1 Los divisores de 15 son ±1, ±3, ±5, ±15
Evaluando el polinomio en estos números comprobamos que ninguno de ellos es raíz del mismo, por lo que el polinomio no tiene raíces enteras.
Entonces las posibles raíces racionales serán los divisores del término independiente (Divisores de 15: ±1, ±3, ±5, ±15) entre los del término de mayor grado (Divisores de 16: ±1, ±2, ±4, ±8, ±16)
Así algunas de las posibles raíces racionales serían: 1, −1, 1/2, −1/2, 1/4, −1/4,...
2 Evaluando el polinomio en dichos números podemos obtener sus raíces racionales y factorizarlo. Observa los siguientes pasos:

por lo que 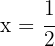 es raiz
es raiz
3Aplicamos el teorema de Fubinni
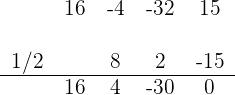
Así, el polinomio se factoriza como

Factorizamos el segundo factor
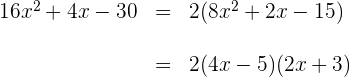
luego el polinomio factorizado queda
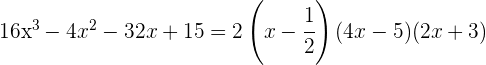
4 Para obtener las raíces igualamos cada factor a cero y despejamos
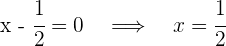


Así, las raíces son 
Si tienes dudas puedes consultar la teoría



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
El valor númerico de la expresión 7(x²-2x+5)/3 , cuando x =-2
-12X-8-3X+10=2X-9+8Y
(2x-1)(3x-5)-6x(2÷3x-1÷2)
10x + 2x
Mesecito ayuda de matemáticas
Puedes obtenerla en https://www.superprof.es/ 🙂
Halla el cociente y el residuo de las divisiones siguientes
(.^3-3.^2+2.-2)\(.+1)
Alguien me ayuda en este problema de polinomios 1. P(x) = 7
2. Q(x) = 4x
2 − 1
3. R(x) = 2x
4 + 5
4. S(x) = x
5 + 2x
2 − 7
5. T(x) = 4x
6 + 2x
3 − 1
6. U(x) = 5x
8