Elige la opción correcta:
1Si 
es raíz del polinomio 
entonces...
Recordemos el Teorema del Factor:
Un polinomio tiene un factor 
si y solo si 
donde es un polinomio de grado 
y 
es cualquier número real.
Por lo tanto si es raiz del polinomio , significa que 
y que es divisible por 
. Esto nos dice que la respuesta correcta es
2Hallar las raíces de un polinomio consiste en...
Recordemos el Teorema del Factor:
Un polinomio tiene un factor si y solo si donde es un polinomio de grado y es cualquier número real.
Es decir, encontrar las raíces de un polinomio significa que y que tiene un factor . Por lo tanto la respuesta correcta es
3Dado un polinomio del tipo 
, podemos afirmar que...
Sea 
una raíz de 
. Entonces tenemos que
de esta ecuación podemos concluir que
Lo cual implica que todas las raíces de dividen a 
4Dado un polinomio del tipo 
, podemos afirmar que...
En cada uno de los sumandos del polinomio aparece la variable 
. Entonces al evaluar el polinomio en 
, tenemos que
Así que el valor es una raíz del polinomio.
5Un polinomio primo es aquel que...
La solución a este problema es muy sencilla, solo debemos recordar la definición de polinomio primo.
Un polinomio que no pueden ser factorizado en polinomios de grado menor, es llamado un polinomio irreducible o primo.
Así que la respuesta correcta es que dicho polinomio primo no puede descomponerse en factores.
6El grado del polinomio que tiene por factorización 
es...
Recordemos que el grado de un polinomio es el mayor exponente que puede aparecer en la variable. En el caso de un polinomio escrito a través de sus factores tenemos que el grado total del polinomio es la suma de los grados de sus factores. Dado que
Podemos concluir que el grado de nuestro polinomio es 
,
7Un ejemplo de polinomio que admite el cero como factor es...
De nuevo recordemos el Teorema del Factor:
Un polinomio tiene un factor si y solo si donde es un polinomio de grado y es cualquier número real.
A la luz de este teorema debemos buscar un polinomio que tenga un factor igual a 
. Por lo tanto el polinomio
nos da la respuesta correcta.
8De los siguientes polinomios aquel que tiene por raíces 
es...
A la luz del teorema del factor debemos buscar un polinomio que tenga como factores a 
, 
y 
. Ahora al analizar las opciones tenemos que
El ultimo polinomio 
nos da la respuesta correcta.
Escoge la opción correcta:
9
tiene...
Debemos evaluar los divisores de 
en 
: 
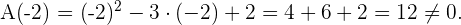
tiene dos raíces simples que son: 
y 
.
El cálculo de las raíces también se puede hacer mediante la fórmula de la ecuación de segundo grado.
10
tiene...
Hallaremos las raíces del polinomio usando el algoritmo de la división. Veremos que is divisible por 
Ahora aplicamos el algoritmo de la division a 
y 
Al obtener cero como residuo podemos concluir que
Ahora debemos analizar el polinomio
Por la formula de la ecuación de segundo grado, podemos concluir que
Por lo tanto
Finalmente podemos decir que el polinomio tiene tres raíces, una raíz doble en 
y otra simple en 
.
Si tienes dudas puedes consultar la teoría
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
no me parece bien que yo ponga mis respuestas bien y salen mal llevo 2 h para 20 de puntuacion y tengo mas bien que mal 0 estrellas
Una disculpa por las fallas, podrías hacernos el favor de indicarnos los números que tienen los ejercicios para poder rectificarlos y dar un mejor servicio.
Buenas Tardes. En el ejercicio 5 posición 10 hay una errata. U(x)
Hola, si te refieres al ejercicio donde U(x) debe ser elevado al cuadrado, ya lo revise y no encontré el error, si me equivoco me lo podrías indicar por favor.
Pues un simple polinómio